Secondary Mechanics/Page5: Linear Motions
Contents
Movements with constant acceleration
Experiment 2.1: accelerating a cart on an inclined plane
We use the same experimental setup as in the experiment 1.1, except that this time the level at which the car is rolling down is even more inclined. We call this a inclined plane. Not only friction is balanced, but also the car is getting faster and faster. The result is an accelerated movement.
Control strip of a movement on the inclined plane, track (A)
Examine the control strip, which is described . by the needle. Whereby do you recognize that the velocity increases in the course of time?
Exercise 2.1: Analysis of the experiment 2.1
Determine the current velocity of the cart at time t = 0.1 s, 0.2-, 0.3-… and compile the results in a diagram! Use two neighbouring needle stitches! Das karierte Papier hat eine Kästchenbreite von 0,50 cm .
Note: The amount of time between two stitches is only 1 / 50 s = 0.02 s, not 1 / 100, as in experiment 1.1, as the electromagnet works with a frequency of 50 Hz.
Now make a proper tv-Diagram of the movement! Consider first the size of axles and their inscription! Solution
Exercise 2.2: experiment 2.1 with a different tilt
Evaluate now, according to exercise 2.1 this second control strip! How did the acceleration change, is it bigger or smaller?
((Control strip of a movement on an differently inclined plane, track (B)))
Theory of the acceleration
We have already seen that the cart which starts on an inclined plane, has the velocity that grows proportional to the time. Consequently the function is:
v(t) = a t
With the constant of proportionality a. We call a the acceleration.
Es folgt in diesem Fall:
[math]a = \frac{v}{t}[/math]
(Bewegung mit konstanten Beschleunigung aus der Ruhe)
Besitzt der Wagen zu Beginn der Bewegung bereits eine Anfangsgeschwindigkeit v0 , so lautet die Funktionsgleichung
v(t) = v0 + a t
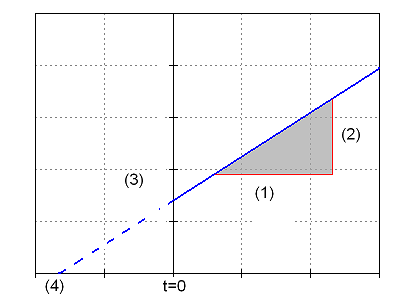
Der Graph ist eine verschobene Ursprungsgerade:
(1)[math]\Delta t[/math]
(2)[math]\Delta v[/math]
(3)v0
(4)t0
Rechtswertachse: Zeit t, Hochwertachse: Geschwindigkeit v
Es ergibt sich für a>0 eine Bewegung mit konstanter Beschleunigung, für a=0 eine Bewegung mit konstanter Geschwindigkeit und für a<0 eine Bewegung mit konstanter Verzögerung (fallende Gerade).
Vorsicht: diesmal ist die Formel [math]a = \frac{v}{t}[/math] falsch!
Es gilt:
[math]a = \frac{\Delta v}{\Delta t}[/math]
a ist also die Steigung der Geraden.
Definition: Die Beschleunigung a ist die Steigung des t-v-Graphen.
Die Einheit der Beschleunigung ist folglich m/s2.
Aufgabe 2.3: Beschleunigungstest
Ein Testinstitut untersucht die Bewegung eines Fahrzeugs. Die Messwerte sind:
| Zeit t in s | Geschwindigkeit v in m/s |
|---|---|
| 0 | 0 |
| 5 | 1 |
| 10 | 2 |
| 60 | 12 |
| 80 | 12 |
| 100 | 12 |
| 110 | 8 |
| 120 | 4 |
| 130 | 0 |
a) Zeichnen Sie ein t-v-Diagramm! (10 s = 1 cm , 1 m/s = 1 cm )
b) Geben Sie die Art der Bewegung in den einzelnen Zeitabschnitten an!
c) Ermitteln sie mithilfe der Zeichnung die Beschleunigungswerte!
Theory for acceleration
We saw that a car, which starts on an inclined level has a speed, which grows proportionally with the time. The function equation reads thus:
v(t) = a t
with the proportionality constant a. We call a acceleration.
It follows in this case:
[math]a = \frac{v}{t}[/math]
(Movement with constant acceleration from the peace.)
If the vehicle is on speed at the beginning of the movement, the equation of the function is:
v(t) = v0 + a t
The graph is a shifted line through origin:
(1)[math]\Delta t[/math]
(2)[math]\Delta v[/math]
(3)v0
(4)t0
x-axis: time t, y-axis: speed v
For a>0 the movement has a constant acceleration, for a=o the movement has a constant speed, and for a<0 the movement has a constant delay (falling line).
!Attention! This time the formula [math]a = \frac{\ v}{\ t}[/math] is wrong!!
To be used is:
[math]a = \frac{\Delta v}{\Delta t}[/math]
a is also the gradient of the line.
Definition: The acceleration a is the gradient of the t-v-line.
The unit of the acceleration is m/s².
Problem 2.3: Accelerationtest
A testinstitution analyses the movement of a vehicle.The results are:
| Time t in s | Speed v in m/s |
|---|---|
| 0 | 0 |
| 5 | 1 |
| 10 | 2 |
| 60 | 12 |
| 80 | 12 |
| 100 | 12 |
| 110 | 8 |
| 120 | 4 |
| 130 | 0 |
a) Draw a t-v-diagramm! (10s=1 cm, 1m/s=1 cm)
b) Name the type of movement in the particular timezones!
c) Find out the accelerations by using the graph!