Mechanics11/Seite6
Contents
Die Zeit-Ort-Funktion bei konstanter Beschleunigung
Und nun wollen wir die Früchte der neuen Theorie ernten: Wir können daraus eine Aussage über den zurückgelegten Weg ableiten!
Wie wir früher gesehen haben, ist der zurückgelegte Weg immer die Fläche unter dem Zeit-Geschwindigkeits-Graphen.
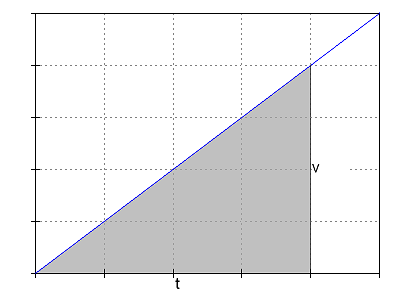Rechtswert: Zeit t, Hochwert: Geschwindigkeit v
Wie aus dem Diagramm zu erkennen ist, gilt für die konstante Beschleunigung aus der Ruhe:
[math]x(t) = \frac{1}{2}t v = \frac{1}{2}t (a t) = \frac{1}{2} a t^2[/math]
[math]x(t) = \frac{1}{2} a t^2[/math]
Interpretation: der zurückgelegte Weg wächst also quadratisch mit der Zeit an. Das heißt zum Beispiel: doppelte Zeit, viermal soviel zurückgelegte Weg!
Der Graph der t-x-Funktion ist also eine Parabel mit der Öffnung [math]\frac{a}{2}[/math] !
Aufgabe 2.4 (Fortsetzung von Aufgabe 2.3)
d) Welche Strecke hat das Fahrzeug beim Erreichen der Höchstgeschwindigkeit zurückgelegt? Welche Strecke liegt es zwischen der 60. und der 100. Sekunde zurück? Welche bis zum Ende der Fahrt?
e) Zeichnen sie das t-x-Diagramm!
Aufgabe 2.5: Überprüfen der Formel
Betrachten Sie noch einmal das Messprotokoll von Versuch 2.1, Spur (A)! Berechnen Sie aus dem Ort und der Zeit des 34. Nadelstiches die Beschleunigung a ! Vergleichen Sie das Ergebnis mit dem Ergebnis von Aufgabe 2.1!
Aufgabe 2.6: Anfahren!
Eine Lokomotive fährt aus dem Stillstand mit der konstanten Beschleunigung a = 0,850 m/s2 an. Nach welcher Zeit hat sie die Geschwindigkeit v = 75,0 km/h erreicht?
Aufgabe 2.7: Von Null auf Hundert
Die Testfahrt eines neuen Motorrads ergab eine Geschwindigkeitszunahme von 0 auf 100 km/h in 3,87 s .
Berechnen Sie die mittlere Beschleunigung und den bei dieser Beschleunigung in dieser Zeit zurückgelegten Weg!
Aufgabe 2.8: Zugfahrt
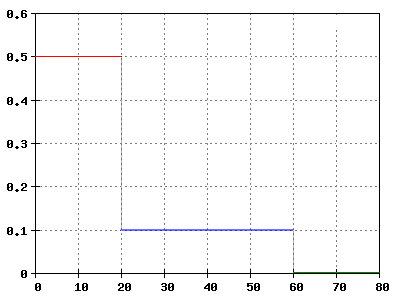
Rechtswert: Zeit t in s
Hochwert: Beschleunigung a in m/s2
Ein Zug fährt an. Die Abhängigkeit seiner mittleren Beschleunigung von der Zeit gibt das Diagramm wieder.
- a) Berechnen Sie die Geschwindigkeiten, die der Zug nach 20 s, 60 s und 80 s hat, und zeichnen Sie das t-v-Diagramm!
- b) Berechnen Sie mithilfe des t-v-Diagramms den zurückgelegten Weg für die gleichen Zeitpunkte und zeichnen Sie das t-x-Diagramm!
Aufgabe 2.9: Gewehrkugel
Die Kugel eines Gewehrs soll im Lauf gleichmäßig beschleunigt werden.
- a) Nach welcher Zeit verlässt die Kugel den Lauf ?
- b) Wie groß ist die Beschleunigung, wenn der 80 cm lange Lauf mit 760 m/s verlassen wird ?
Aufgabe 2.10: Kavaliersstart?
Beim Anfahren eines Wagens nimmt man folgende Meßreihe auf :
| Zeit t in s | Ort x in m |
|---|---|
| 0 | 0 |
| 1 | 0,5 |
| 2 | 2 |
| 3 | 4,5 |
| 4 | 8 |
| 4,2 | 8,8 |
| 5 | 12 |
| 6 | 16 |
| 7 | 20 |
- a) Mit welchen Weg-Zeit-Funktionen lassen sich die Bewegungen in den Zeitabschnitten 0 < t < 4 s und 4 s < t < 7 s beschreiben?
- b) Bestimmen Sie die Beschleunigung und die Momentangeschwindigkeit für jeden Punkt der Tabelle! Zeichnen Sie das v(t)-Diagramm! Bestimmen Sie daraus mit Hilfe der Fläche den Ort x(6,5 s) zu t = 6,5 s!
