Mechanics11/Seite4
Contents
Guter Stil beim Rechnen
Beachten Sie bei Rechenaufgaben den “guten Stil”:
- 1. Bereitstellen der relevanten Formeln
- 2. Ansatz
- 3. Auflösen nach der/den Unbekannten
- 4. Einsetzen der Zahlen
- 5. Ausrechnen
- 6. Runden (auf die geringste Genauigkeit der gegebenen Größen, +/- eine Stelle)
Für fehlende Schritte müssen in Prüfungen leider Punkte abgezogen werden!
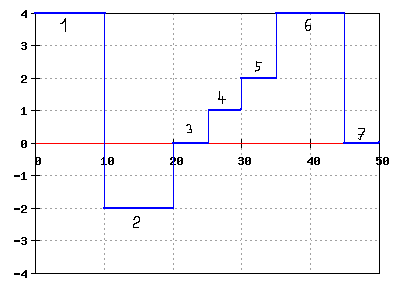
Aufgabe 1.7: Hürdensprung
Diana springt mit ihrem Pferd über ein Hindernis und ihr Trainer nimmt die Bewegungsdaten mit einem Lasermessgerät auf. Die Daten werden auf einem Computerbildschirm, etwas idealisiert, als t-v-Diagramm und t-x-Diagramm dargestellt. Mit Hilfe dieser Diagramme können Trainer und Reiterin die Bewegung analysieren.
Zuerst galoppiert Helena auf ihrem Pferd mit konstanter Geschwindigkeit auf das Hindernis zu (1), bis das Pferd plötzlich scheut und rückwärts geht (2). Helena hält es an (3), setzt noch einmal an und steigert die Geschwindigkeit. Bei 40 s springt das Pferd (6) und nach der Landung kommt es wieder zum Stehen (7).
Rechtswertachse: Zeit in s, Hochwertachse: Geschwindigkeit des Pferdes in m/s
- a) Berechnen Sie die Position x des Pferdes im Verlauf der Zeit t! Benützen Sie dazu geeignete Berechnungsformeln! (Formel, Umformen, Einsetzen, Ausrechnen, auf die Einheiten achten!)
- b) Zeichnen Sie das Zeit-Orts-Diagramm des Pferdes!
(Hinweis: An der Fläche unter dem Geschwindigkeitsgraphen lässt sich wegen [math]\Delta x[/math] = v[math]\Delta t[/math] auch leicht der zurückgelegte Weg direkt ablesen!)
Aufgabe 1.8: Messprotokoll
Ein Fahrzeug bewegt sich auf geradliniger Bahn. Man erhält folgende Messreihe :
t in s..............4,2.....7,5......9,0.......12,7........14,0
x in m...........12,0....74,1...93,6.....152,4......178,6
- a) Zeichnen Sie das zugehörige t-x-Diagramm ! (1 s = 1 cm ; 1 m = 1 mm)
- b) Gehen Sie davon aus, dass es sich um eine gleichförmige Bewegung handelt. Bestimmen Sie ihre Geschwindigkeit! (Tipp: Was wissen wir über den Ort des Fahrzeugs zur Zeit t = 0 ?)
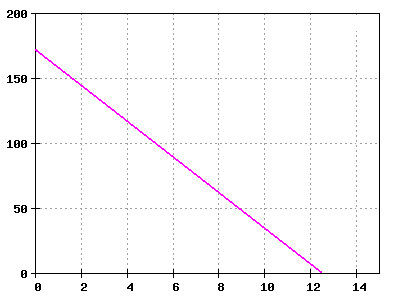
Aufgabe 1.9: Rückwärtsgang
Berechnen Sie aus dem in der untenstehenden Abbildung wiedergegebenen t-x-Diagramm einer idealen Bewegung, die wir uns beliebig lange fortgesetzt denken können,
- a) die Fahrzeuggeschwindigkeit,
- b) die Koordinate x1 des Ortes, den das Fahrzeug zur Zeit t1 = 2 min 53 s hat,
- c) die Zeit t2, zu der es am Ort mit der Koordinate x2 = - 6,2 km ist!
Es gilt: Start bei 168 m , x = 0 nach 12,5 s .
Rechtwertachse: Zeit in s , Hochwertachse: Ortskoordinate in m .
Aufgabe 1.10: Eingeholt!
Ein LKW fährt auf einer geraden Straße mit der konstanten Geschwindigkeit v1 = 45 m/s von dem Ort mit der Koordinate 47,7 km ab. Ein PKW fährt 70 s später ebenfalls mit konstanter Geschwindigkeit von dem Ort mit der Koordinate 15,2 km ab ; beide fahren in Richtung wachsender Ortskoordinaten. Der PKW holt den LKW 1 h 20 min nach dem Start des PKW ein.
- a) Fertigen Sie ein qualitatives t-x-Diagramm!
- b) Welche Geschwindigkeit v2 hat der PKW?
- c) Welche Strecken haben beide Fahrzeuge bis zum Treffen zurückgelegt ?
Beachten Sie den „guten Stil“!
Aufgabe 1.11: Geblitzt!
Die Bewegung eines Autos wird von einem “Radargerät“ erfasst, das mit Ultraschall arbeitet.
Dazu wird zum Zeitpunkt t1 = 0,65 s ein Schallimpuls ausgesandt, der nach der Reflexion am Auto zu Zeit t2 = 0,95 s wieder am Gerät eintrifft. Dieses befindet sich am Ort x = 0 .
Ein zweiter Impuls wird zur Zeit t3 = 3,80 s ausgesandt und kommt zur Zeit t4 = 4,80 s zurück.
Die Geschwindigkeit v des Autos bleibt dabei die ganze Zeit konstant.
a) Zeichnen Sie ein qualitatives t-x-Diagramm des Vorgangs! (Keine Zahlenwerte!)
Tragen Sie dazu die Zeit-Orts-Linien der Schallimpulse sowie des Autos ein!
b) Berechnen Sie aus den gegebenen Werten und der Schallgeschwindigkeit vs = 340 m/s die Geschwindigkeit v des Autos in km/h !
c) Ermitteln Sie zeichnerisch oder rechnerisch die Position des Autos zur Zeit t = 0 !
Aufgabe 1.12 Streckenposten
Bei einer Leichtathletik-Meisterschaft kommt Läuferin A mit einer konstanten Geschwindigkeit von 27,2 km/h an einem Streckenposten vorbei. 2,5 Sekunden später passiert Läuferin B den Posten mit einer konstanten Geschwindigkeit von 30,4 km/h. Ermitteln Sie zeichnerisch und rechnerisch, wann und wo Läuferin A von Läuferin B überholt wird!