User:Peanut3m11

hi my name is jakob and i go in class 11. because of my physics-course I`m here and we make here our homeworks and some lessons. cu

sandbox

Aufgabe 1.7
a) x(t) = x₀+ v [math]\Delta[/math]t

[math]\frac {x(t)-x_0}{v}[/math] = [math]\Delta[/math]t
Falke: x(t) = 0km + 153[math]\frac {km}{h}[/math][math]\Delta[/math]t
Bussard: x(t) = 14km + 95[math]\frac {km}{h}[/math][math]\Delta[/math]t
(153t)h=(14+95t)h
t=0,24h -->Einsetzten--> x=37km

Lew in Zusammenarbeit mit Jakob und David:

Ein Jogger und ein Radler wollen beide in den englischen Garten Der Radler mit der Geschwindigkeit 20km/h holt den Jogger nach 12 min ein . Wer kommt wann am 8,9km entfernten Chinesischen Turm an, wenn beide am gleichen Ort mit konstanter Geschwindigkeit starten?

Löse rechnerisch und graphisch!

---

Aufgabe 4.7

a) E=[math]\frac {1}{2}[/math]mv²
-->[math]\frac {1}{2}[/math]*2000kg*50[math]\frac {km}{h}[/math]=193kJ
b) E=mgh
-->1000kg*9.61[math]\frac {n}{kg}[/math]*200m=1,96MJ
c) E=[math]\frac {1}{2}[/math]mv²
-->[math]\frac {1}{2}[/math]*4000t*1[math]\frac {m}{s}[/math]="MJ

---

Aufgabe 4.8

a) E=[math]\frac {1}{2}[/math]mv²
-->(5,0[math]\frac {m}{s}[/math]*[math]\frac {1}{2}[/math]*70g=0,88J
E=mgh
-->7g*9,81[math]\frac {N}{kg}[/math]*200m=1,96MJ
E=0,88J-0,69J=0,19J
V=[math]\sqrt{\frac{0,19J}{2*0,07kg}}[/math]=1,2[math]\frac {m}{s}[/math]
b) 5,0[math]\frac {m}{s}[/math]
c)siehe Lsg wie in a)

---

aufgabe von jakob feat lew

Kugelstoßen
Eine Kugel der Masse 100g rollt auf eine Rampe zu, sie hat die Geschwindigkeit 17km/h.Sie rollt die Rampe 1,83m runter auf eine plane Ebene.Nach der Ebene rollt sie eine weitere Rampe 0,49m hoch. Oben befindet sich eine Ebene mit einer Feder der Federhärte 2,8 N/cm. Wie weit wird die Feder gestaucht?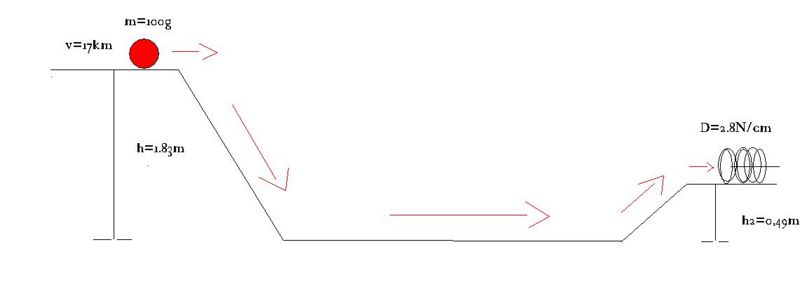

--- ==Aufgabe 5.1==

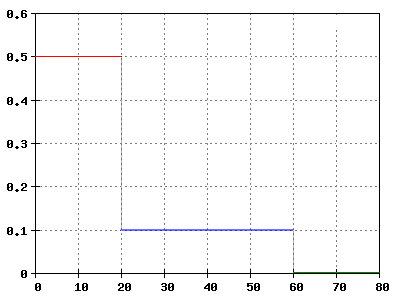
Aufgabe 2.8: Zugfahrt

[1]

Rechtswert: Zeit t in s
Hochwert: Beschleunigung a in m/s²

Ein Zug fährt an. Die Abhängigkeit seiner mittleren Beschleunigung von der Zeit gibt das Diagramm wieder.

• a) Berechnen Sie die Geschwindigkeiten, die der Zug nach 20 s, 60 s und 80 s hat, und zeichnen Sie das t-v-Diagramm!
• b) Berechnen Sie mithilfe des t-v-Diagramms den zurückgelegten Weg für die gleichen Zeitpunkte und zeichnen Sie das t-x-Diagramm!

Lösung:

a)

[math]v(t)_1= a_1*t_1= 0,5 \frac {m} {s^2}*20s= 10 \frac {m} {s} [/math]

[math]\Delta v(t)_2= a_2*\Delta t_2= 0,1 \frac {m} {s^2}*40s= 4 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

[math]\Delta v(t)_3= a_3*\Delta t_3= 0 \frac {m} {s^2}*40s= 0 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

---

Aufgabe 2.9: Gewehrkugel

Die Kugel eines Gewehrs soll im Lauf gleichmäßig beschleunigt werden.

• a) Nach welcher Zeit verlässt die Kugel den Lauf ?
• b) Wie groß ist die Beschleunigung, wenn der 80 cm lange Lauf mit 760 m/s verlassen wird ?

Lösung:

a)

[math] x(t)= \frac {1}{2}a*t^2 =\gt t= 2 \frac {x(t)} {v}= 2\frac {0,8m} {760m/s}= \frac {21} {10000} s[/math]

b)

[math] a= \frac {\Delta v} {\Delta t} =\gt a= \frac {760 m/s} {\frac {21} {10000} s}= 361000 \frac {m} {s^2}[/math]

Aufgabe 2.10: Kavaliersstart?

hier wird einst eine lösung stehen..

Aufgabe 3.10: Landetraining?

[math]t= 7.5 \frac {m} {s}[/math]
[math]v=a*t[/math]
[math] t= \frac {v}{a} = \frac {7,5}{9.81}s = 0,764s[/math]
[math] h = \frac {1}{2}g*t^2 = \frac {1} {2}*0,764^2*9,81=2.81m[/math]

Aufgabe Fallschirmspringer

Ein Fallschrimspringer springt in 4000 m Höhe bei der Zeit (t=0) aus einem Flugzeug. Für die nächsten 1000 m braucht er 25,95 s. Er fällt mit konstanter Geschwingkeit.

    a) Auf Welcher Höhe befindet er sich nach 85,49s?
    b) Bei 85,49s zieht er die Reißleine des Fallschirms und erreicht dann eine konstante
        Geschwidigkeit von 20 km/h. Wie viel Zeit benötigt er bis zum Boden?
    c) Berechne die durchschnittliche Geschwindigkeit.
    d) Wie viel Zeit würde er benötigen wenn er die Reißleine bei 500m Höhe ziehen würde
       (mit selber Geschwindigkeit)
    e) Zeichne ein passendes Zeit-Ort Diagramm.

Aufgabe erstellt von : Rambotürke^M11 , Julian und SchraffelM11

Aufgabe 2.7: Von Null auf Hundert

Die Testfahrt eines neuen Motorrads ergab eine Geschwindigkeitszunahme von 0 auf 100 km/h in 3,87 s.

    a) Berechnen sie die mittlere Beschleunigung und den bei dieser Beschleunigung
       in dieser Zeit zurückgelegten Weg!

t= 3,87s

v(t)=a*t

[math]x(t)= \frac {v(t)} {t} = \frac {27,78 m/s} {3,87s} = 7,12 \frac {m} {s^2} [/math]
[math]x(t)= \frac {1} {2} *7,12 \frac {m} {s^2}*(3,87s)^2= 53,75m [/math]

Aufgabe 2.6: Anfahren

Eine Lokomotive fährt aus dem Stillstand mit der konstanter Beschleunigung a = 0,850 m/s² an.

    a) Nach welcher Zeit hat sie die Geschwindigkeit v = 75,0 km/h erreicht?

[math]a= 0,850 \frac {m} {s^2} [/math]

Gesucht: Nach welche Zeit gilt: [math]v= 75,0 \frac {km} {h} [/math]

Lösung: [math]a= \frac {\Delta v} {\Delta t} [/math]

=> Nach [math]\Delta t[/math] auflösen und einsetzen

[math]\Delta t= \frac {\Delta v} {a} = \frac {75 km/h} {0,850 m/s^2} = \frac {20,83m/s} {0,850 m/s^2} = 24,50 s [/math]

Aufgabe 1.6: Wettflug

Ein Bussard fliegt mit einem Falken um die Wette. Der Bussard bekommt 14 km Vorsprung vom Startpunkt aus gemessen, weil er mit 95 km/h deutlich langsamer ist als der Falke (153 km/h).

    a) Wann und wo holt der Falke den Bussard ein?
    b) Wer gewinnt den Wettflug bis zum Gipfelkreuz des Hörnle (40km vom Statr entfernt)

[math]V_B= 95 \frac {km} {h} [/math]

[math]V_F = 153 \frac {km} {h}[/math]

a)

[math]x(t)= 0km+153\frac{km}{h}*t[/math]
[math]x(t) = 14km+95\frac{km}{h}*t[/math]
[math]153\frac{km}{h}*t = 14km+95\frac{km}{h}[/math]
[math]58\frac{km}{h}*t = 14km[/math]

[math]=\gtt = 0,24h[/math]

t einsetzten :

[math]x(t) = 0km+153\frac{km}{h}*0,24h = 37km[/math]

b)

Der Falke gewinnt, da er den Bussard bereits überholt hat bevor das Rennen zu Ende ist.

Aufgabe 3.11: Verweis!

    Eine Schülerin des Gisela-Gymnasium lässt einen Schneeball aus dem 3. Stock
    (Stockwerkshöhe 3,45m) in den Schulhof fallen.
    a) Wie lang ist die Fallzeit?
    b) Mit welcher Geschwindigkeit kommt er unten an?
    c) Berechnen Sie Fallzeit und Endgeschwindigkeit für einen Fall aus der
       gleichen Höhe auf dem Mond! (Dort ist die Gravitationsfeldstärke nur
       1/7 so groß wie auf der Erde.)

a) h= 4*3,45m

[math]t= \sqrt {\frac {2h} {g}} = 1,67s[/math]

b) [math]v^2=2gh[/math]
[math]v=\sqrt {\frac {2h} {g}}=16,4 \frac {m}{s}[/math]= 59 \sqrt {\frac {km} {h}}