User:Rambotürke^M11

Hi, im Tobias and i am a 17 year old student at the gisela gymnasium, a school in munich/ germany, we are in here because of the physic lessons.

Aufgabe 1.6: Wettflug

Ein Bussard fliegt mit einem Falken um die Wette. Der Bussard bekommt 14 km Vorsprung vom Startpunkt aus gemessen, weil er mit 95 km/h deutlich langsamer ist als der Falke (153 km/h).

    a) Wann und wo holt der Falke den Bussard ein?
    b) Wer gewinnt den Wettflug bis zum Gipfelkreuz des Hörnle (40km vom Statr entfernt)

[math]V_B= 95 \frac {km} {h} [/math]

[math]V_F = 153 \frac {km} {h}[/math]

a)

[math]x(t)= 0km+153\frac{km}{h}*t[/math]
[math]x(t) = 14km+95\frac{km}{h}*t[/math]
[math]153\frac{km}{h}*t = 14km+95\frac{km}{h}[/math]
[math]58\frac{km}{h}*t = 14km[/math]

[math]=\gtt = 0,24h[/math]

t einsetzten :

[math]x(t) = 0km+153\frac{km}{h}*0,24h = 37km[/math]

b)

Der Falke gewinnt, da er den Bussard bereits überholt hat bevor das Rennen zu Ende ist.

Aufgabe 2.6: Anfahren

Eine Lokomotive fährt aus dem Stillstand mit der konstanter Beschleunigung a = 0,850 m/s² an.

    a) Nach welcher Zeit hat sie die Geschwindigkeit v = 75,0 km/h erreicht?

[math]a= 0,850 \frac {m} {s^2} [/math]

Gesucht: Nach welche Zeit gilt: [math]v= 75,0 \frac {km} {h} [/math]

Lösung: [math]a= \frac {\Delta v} {\Delta t} [/math]

=> Nach [math]\Delta t[/math] auflösen und einsetzen

[math]\Delta t= \frac {\Delta v} {a} = \frac {75 km/h} {0,850 m/s^2} = \frac {20,83m/s} {0,850 m/s^2} = 24,50 s [/math]

Aufgabe 2.7: Von Null auf Hundert

Die Testfahrt eines neuen Motorrads ergab eine Geschwindigkeitszunahme von 0 auf 100 km/h in 3,87 s.

    a) Berechnen sie die mittlere Beschleunigung und den bei dieser Beschleunigung
       in dieser Zeit zurückgelegten Weg!

t= 3,87s

v(t)=a*t

[math]x(t)= \frac {v(t)} {t} = \frac {27,78 m/s} {3,87s} = 7,12 \frac {m} {s^2} [/math]
[math]x(t)= \frac {1} {2} *7,12 \frac {m} {s^2}*(3,87s)^2= 53,75m [/math]

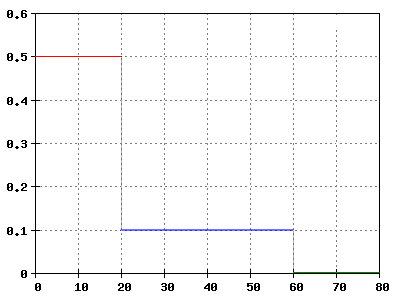
Aufgabe 2.8: Zugfahrt

[1]

Rechtswert: Zeit t in s
Hochwert: Beschleunigung a in m/s²

Ein Zug fährt an. Die Abhängigkeit seiner mittleren Beschleunigung von der Zeit gibt das Diagramm wieder.

• a) Berechnen Sie die Geschwindigkeiten, die der Zug nach 20 s, 60 s und 80 s hat, und zeichnen Sie das t-v-Diagramm!
• b) Berechnen Sie mithilfe des t-v-Diagramms den zurückgelegten Weg für die gleichen Zeitpunkte und zeichnen Sie das t-x-Diagramm!
  

[math]\Delta v(t)_3= a_3*\Delta t_3= 0 \frac {m} {s^2}*40s= 0 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

Aufgabe 2.9: Gewehrkugel

Die Kugel eines Gewehrs soll im Lauf gleichmäßig beschleunigt werden.

• a) Nach welcher Zeit verlässt die Kugel den Lauf ?
• b) Wie groß ist die Beschleunigung, wenn der 80 cm lange Lauf mit 760 m/s verlassen wird ?

Lösung:

a)

[math] x(t)= \frac {1}{2}a*t^2 =\gt t= 2 \frac {x(t)} {v}= 2\frac {0,8m} {760m/s}= \frac {21} {10000} s[/math]

b)

[math] a= \frac {\Delta v} {\Delta t} =\gt a= \frac {760 m/s} {\frac {21} {10000} s}= 361000 \frac {m} {s^2}[/math]

Aufgabe 3.10: Landetraining

    Ein Fallschirmspringer kommt mit einer Geschwindigkeit von 7,5 m/s auf den Boden auf.
    Zum Training springt er zunächst von einer Plattform. Wie hoch muss diese sein, damit
    er mit der gleichen Geschwindkeit aufkommt?

Lösung:

a)

[math]v(t)_1= a_1*t_1= 0,5 \frac {m} {s^2}*20s= 10 \frac {m} {s} [/math]

[math]\Delta v(t)_2= a_2*\Delta t_2= 0,1 \frac {m} {s^2}*40s= 4 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

[math]t= 7.5 \frac {m} {s}[/math]
[math]v=a*t[/math]
[math] t= \frac {v}{a} = \frac {7,5}{9.81}s = 0,764s[/math]
[math] h = \frac {1}{2}g*t^2 = \frac {1} {2}*0,764^2*9,81=2.81m[/math]

Aufgabe 3.11: Verweis!

    Eine Schülerin des Gisela-Gymnasium lässt einen Schneeball aus dem 3. Stock
    (Stockwerkshöhe 3,45m) in den Schulhof fallen.
    a) Wie lang ist die Fallzeit?
    b) Mit welcher Geschwindigkeit kommt er unten an?
    c) Berechnen Sie Fallzeit und Endgeschwindigkeit für einen Fall aus der
       gleichen Höhe auf dem Mond! (Dort ist die Gravitationsfeldstärke nur
       1/7 so groß wie auf der Erde.)

a) h= 4*3,45m

[math]t= \sqrt {\frac {2h} {g}} = 1,67s[/math]

b) [math]v^2=2gh[/math]
[math]v=\sqrt {\frac {2h} {g}}=16,4 \frac {m}{s}= 59 \frac {km} {h}[/math]
c) [math] v'= \sqrt {2*1/7*g*h}=6,2 \frac {m} {s} [/math]
[math]t'=4,4s[/math]

Aufgabe 4.3: Spann die Feder!

    Eine zunächst entspannte Stahlfeder wird durch eine Kraft von 50 N um 80 cm gedehnt.
         a) Welche Spannarbeit ist dazu erforderlich?
         b) Welche zusätzliche Spannarbeit muss an der Feder verrichtet werden um sie weitere 50 cm auszudehnen?
         c) Welche Spannenergie steckt nun in der Feder?

Aufgabe 4.6: Enegievergleich

    Berechnen Sie die Energie
         a) eines Kleinbusses von 2.0 t Masse bei einer Geschwindigkeit von 50 km/h.
         b) von 1,0 m³ Wasser in einer Höhe von 200m ( Walchenseekraftwerk )
         c) von 4000 m³ Wasser im Rhein, wenn die Fließgeschwindigkeit 1,0 m/s beträgt!
    Welche Art von Energie liegt jeweils vor?

a) m= 2,0t; v= 50km/h

[math] E_k = 0,5 m*v^2 = 0,5*2000kg*13,9= 192,9kJ [/math]

b) [math]V= 1,0m^3; h= 200m[/math]
[math]=\gt m= 1000kg[/math]
[math]E_H= m*g*h= 1000[/math]kg[math]*9,81 N/[/math]kg[math]*200m= 1962000J= 1962kJ[/math]
c) [math]V= 4000m^3; v= 1,0 m/s; m= 4000000kg= 4000t[/math]

[math]E_K= 0,5mv^2= 0,5*4000000kg*1^2= 2000kJ= 2,0MJ[/math]

Aufgabe 4.7: Hell racer

    Ein Spielzeugauto der Masse 70g fährt auf einer horizontalen Bahn mit der konstanten Geschwindigkeit 5,0 m/s.
    Anschließend durchfährt es einen senkrechten Halbkreis mit Radius 50cm.
    Die Reibung darf vernachlässigt werden.
    a)Mit welcher kinetischer Energie und mit welcher Geschwindigkeit verlässt das Auto den Halbkreis?
    b)Mit welcher Geschwindigkeit erreicht es wieder die horizontale Bahn?
    c)Das selbe Auto wird mit 5,0 m/s senkrecht nach oben geworfen. Welche Geschwindigkeit besitzt es in 1,0 m Höhe?

[math]m= 70g= 0,07kg ; v=5,0 \frac {m}{s} [/math]
a) E_pot[math]=m*g*h= 0,07kg*9,81\frac {N} {kg}*1m= 0,89J [/math]
E_kin[math]=\frac {1} {2}m*v^2= 0,875J[/math]
E_kin2 = E_kin - E_H = 0,19J

b) [math]v= \sqrt {\frac {2E} {m} } = 2,33 \frac {m} {s} [/math]

c) [math]v= 5,0 \frac {m} {s} h=1,0m[/math]
[math]x(t)= \frac {1} {2}a*t^2[/math]
[math]t= 0,45s[/math]
[math]v=[/math]v₀[math]-g*t= 0,57 \frac {m} {s}[/math]

Aufgabe 5.7: Dosenflug

Eine Getränkedose wird an einer Schnur auf einem vertikalen Kreis mit dem Radius 1,0 m herumgeschleudert.

     a) Welche Geschwindigkeit hat die Dose im höchsten Punkt, wenn die Schnur dort gerade noch gespannt ist?
     b) Wie groß ist diesem Fall die Geschwindigkeit im tiefsten Punkt der Bahn?
     c) Wie hoch kann die Dose fliegen, wenn man die Schnur los lässt?

[math]a) r= 1,0m[/math]
[math]v= \sqrt {g*r}= \sqrt {9,81N/kg*1m}= 3,13m/s[/math]

[math]b) v= \sqrt {v_0^2+2g2r}= \sqrt {(3,13m/s)^2+2*9,81N/Kg*2*1m}= 9,40m/s[/math]
[math]c) [/math]

Aufgabe 5.6: Schleuderball mit Tücken

Ein Ball der Masse 0,80 kg wird an einer 50 cm langen Schnur auf einem vertikal stehenden Kreis herumgeschleudert.

     a) Berechnen Sie die Zentralkraft, die Schnur im höchsten und im tiefsten Punkt der Bahn auf ihn ausübt,
        wenn die Umlaufgeschwindigkeit konstant 3,4 m/s beträgt!

Nun wird der Ball auf einem waagrechten Kreis immer schneller geschleudert.

     b) Bei welcher Frequenz reißt die Schnur, wenn die Reißfestigkeit  50  N beträgt?
     c) Mit welcher Geschwindigkeit fliegt der Ball dann waagrecht weg?

[math]a) m=0,8kg; r=50cm = 0,5m; v_u= 3,4 \frac {m} {s}[/math]
[math]F_Z= m*(omega)^2*r= m \frac {v_2^2} {r}[/math]

Aufgabe Fallschirmspringer

Ein Fallschrimspringer springt in 4000 m Höhe bei der Zeit (t=0) aus einem Flugzeug. Für die nächsten 1000 m braucht er 25,95 s. Er fällt mit konstanter Geschwingkeit.

    a) Auf Welcher Höhe befindet er sich nach 85,49s?
    b) Bei 85,49s zieht er die Reißleine des Fallschirms und erreicht dann eine konstante
        Geschwidigkeit von 20 km/h. Wie viel Zeit benötigt er bis zum Boden?
    c) Berechne die durchschnittliche Geschwindigkeit.
    d) Wie viel Zeit würde er benötigen wenn er die Reißleine bei 500m Höhe ziehen würde
       (mit selber Geschwindigkeit)
    e) Zeichne ein passendes Zeit-Ort Diagramm.

Aufgabe erstellt von : Rambotürke^M11 , Julian und SchraffelM11