User:Chela5808/My sandbox Sam3 HandStyled

Before Styling	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5	Sample 6
After Styling	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5	Sample 6

Styling by hand Sample 3

• Text: Wiki Markup;
• Formulae: [math]\mathrm{L\!\!^{{}_{\scriptstyle A}} \!\!\!\!\!\;\; T\!_{\displaystyle E} \! X} \,[/math] some took directly from corresponding .tex file.

Comments:

• Hand styling time : 1 hour

0.1 Using vectors in 3-space

In ordinary algebraic number theory (Book 1, Chapter 4) we represented numbers by points on a straight line, or with the displacements which lead from an origin to these points. The displacements are in fact vectors in a 1-space, each being a numerical multiple of a unit ‘step’ which we called [math]\mathsf{e}\,[/math]; and any 1-vector [math]\mathsf{a}\,[/math] is written as [math]\mathsf{a} = a\mathsf{e}\,[/math], where [math]a\,[/math] is just a number saying ‘how many’ steps we take in the direction of [math]\mathsf{e}\,[/math]. Of course, if [math]a\,[/math] is an integer, the displacement will lead to a point labelled by that integer; but we know from Book 1 that this picture can be extended to the case where [math]a\,[/math] is any real number and [math]\mathsf{a}\,[/math] is the vector leading to its associated point in the pictorial representation. The rules for combining vectors in 1-space are known from Book 1: we get the sum of two displacements, [math]\mathsf{a}\,[/math] and [math]\mathsf{b}\,[/math], by making them one after the other (the end point of the first being the starting point for the second) and it doesn’t matter which way round we take them. Thus

[math]\mathsf{a}+\mathsf{b}=\mathsf{b}+\mathsf{a}\,[/math]

(3)

and if there are three vectors it doesn’t matter how we combine them,

[math](\mathsf{a}+\mathsf{b})+\mathsf{c}=\mathsf{a}+(\mathsf{b}+\mathsf{c})\,[/math]

(4)

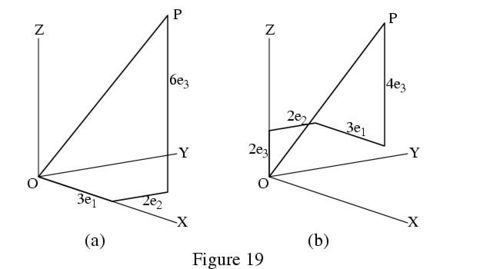
We can also multiply a vector by any real number, as in writing [math]\mathsf{a}\,[/math] as a number [math]a\,[/math] of units [math]\mathsf{e}\,[/math]: [math]\mathsf{a} = a\mathsf{e}\,[/math]. Let’s try to do the same things in 3-space. There will now be three different kinds of unit step – along the x-axis, the y-axis, and the z-axis – which we’ll call [math]\mathsf{e}_1,\mathsf{e}_2,\mathsf{e}_3,\,[/math] respectively. They will be the basis vectors of our algebra and we take them to be of unit length (being ‘unit steps’) A vector pointing from the origin [math]\mathsf{O}\,[/math] to point [math]\mathsf{P}(x, y,z)\,[/math]

(i.e. with Cartesian coordinates [math]x,y,z\,[/math]) will be denoted by [math]r\,[/math] and written

[math]r=x\mathsf{e}_1+y\mathsf{e}_2+z\mathsf{e}_3\,[/math]

(5)

This is really just a rule for getting from [math]\mathsf{O}\,[/math] to [math]\mathsf{P}\,[/math]: If the coordinates are integers e.g. [math]x=3\,[/math], [math]y=2\,[/math], [math]z=6\,[/math], this reads “take 3 steps of type [math]\mathsf{e}_1\,[/math] , 2 of type [math]\mathsf{e}_2\,[/math] and 6 of type [math]\mathsf{e}_3\,[/math] – and you’ll be there!” And the remarkable fact is that, even although the terms in (??) are in different directions, the order in which we put them together doesn’t make any difference: you can take 2 steps parallel to the z-axis (type [math]\mathsf{e}_3\,[/math]), then 2 steps parallel to the y-axis (type [math]\mathsf{e}_2\,[/math] ), 3 more steps of type [math]\mathsf{e}_1\,[/math] , and finally 4 steps of type [math]\mathsf{e}_3\,[/math] – and you’ll get to the same point. This is easy to see from Fig.19, remembering that (because the axes are perpendicular ) space is being ‘marked out’ in rectangles, whose opposite sides are equal. In fact, the rules (??) and (??) apply generally for vector addition.