Secondary Mechanics/Page3: Linear Motions
Exercise 1.5: Bike trip
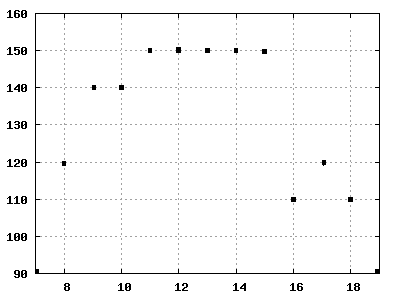
Desiree and Marc want to cycle to the Plansee. They start their ride at 7:00 and come back home at 19:00. The street is flanked with kilometre-marks. Each hour they note their position x.
vertical line: time in hours, horizontal line: coordinates of place in kilometres
- a) Calculate the speed of every time-interval of 1 hour. Utilise the calculation-formula!
- b) Describe the process of movement for every time intervall in words. Interpretation?
- c) Compute the average velocity for the first 4 hours! How could you epitomise this graphically?
--Lenny 12:52, 16 November 2007 (CET)
[math]v = \frac{\Delta x}{\Delta t} = \frac{x - x_0}{\Delta t}[/math]
x = x0 + v[math]\Delta t[/math]
With that you can calcutate the actual position after each time interval with known startpoint x and known velocity v . If we take [math]x_0[/math] for the place x(0) at the time t = 0, we gain the
1.motion equation:
x(t)= x0 + v t
It concerns of a liner equation. In mathematics we always write:
y(x) = t + mx
X is the independent and y the dependent variable. T is the so-called y-axisigment and m the upward gradient factor("gradient"). In the motion equation the independent variable of time is t, the place x depends on it. The velocity v is the upward gradient of the time-localstraight.
Exercise 1.6: Flight competition
A buzzard has a flying competition against a falcon. The buzzard has an advantage of 14 km from the starting point, because with the speed of 95 km/h he is clearly slower than the falcon ( 153 km/h)
a.
Where and at what time does the falcon overtake the buzzard?
b.
Who wins the flight competition to the cross on the summit of the Hörnle (40 km from the starting point).
c.
Draw an applicative time-place diagramm.
--Lenny 12:49, 16 November 2007 (CET) --Benni.m 12:50, 16 November 2007 (CET)