Mechanics11/Seite2

zurück zur vorigen Seite

Um eine Bewegung zu messen, brauchen wir eine

• Ortskoordinate x und eine
• Zeitkoordinate t.

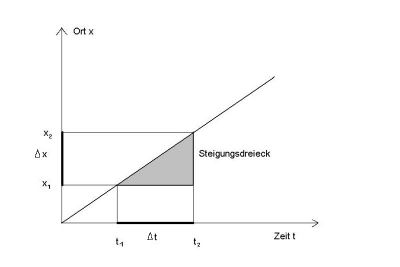
Der Ortsunterschied ist dann Delta x:
[math]\Delta x[/math] = x₂ - x₁

(Ortskoordinate am Ende minus Ortskoordinate am Anfang des Zeitintervalls)

Entsprechend das Zeitintervall [math]\Delta t[/math]:
[math]\Delta t[/math] = t₂ - t₁

Damit wird die Geschwindigkeit

Definition

v = [math]\frac{\Delta x}{\Delta t}[/math]

(zurückgelegte Strecke durch dazu benötigte Zeit)

Hinweis: Hier handelt es sich um einen Quotienten aus Differenzen, einen Differenzenqoutienten.

Nehmen wir zwei benachbarte Messpunkte, so erhalten wir die Momentangeschwindigkeit des Wägelchens zum Zeitpunkt t₁ bzw. t₂, nehmen wir den ersten und den 51. Messpunkt, erhalten wir die Durchschnittsgeschwindigkeit im Zeitintervall

[math]\Delta t[/math] = t₅₁ - t₁

Die Bewegung lässt sich graphisch darstellen in einem Zeit-Orts-Diagramm (t-x-Diagramm):

Konstante Geschwindigkeit

Aufgabe 1.2: Diagramm

Zeichnen Sie je ein Zeit-Ort-Diagramm für Wägelchen A und B ! Wählen Sie die Einheiten geeignet!

Lösung

Aufgabe 1.3: Schneckenpost

Zwei Schnecken bewegen sich gleichförmig und geradlinig in einem Garten:
die erste Schnecke bewegt sich mit 1 mm/s , die zweite in 2 s um 4 mm .
Nach 2 s bleibt die zweite Schnecke aber plötzlich stehen.
Wenn die erste Schnecke die zweite überholt, verdoppelt sie ihre Geschwindigkeit, während die zweite mit halber Anfangsgeschwindigkeit weiter kriecht.
a) Zeichnen Sie ein gemeinsames x-t-Diagramm !
(1s = 1 cm ; 1 mm = 1 cm)
b) Stellen Sie die Abhängigkeit der Geschwindigkeiten von der Zeit für beide Bewegungen in einem Diagramm dar !
(1 s = 1 cm; 0,5 mm/s = 1 cm.)

Tipp

Lösung zu a)

Aufgabe 1.4: Fahrstile

Eine Strecke von 300 km soll mit einem Wagen zurückgelegt werden. Berechnen Sie die dazu benötigte Zeit, wenn

• a) die Geschwindigkeit immer 75 km/h beträgt,
• b) eine Hälfte des Weges mit 50 km/h, die andere mit 100 km/h zurückgelegt wird,
• c) die halbe Fahrzeit mit 50 km/h , die andere mit 100 km/h gefahren wird. (Lösung z.B. durch Erraten und anschließende grafische oder rechnerische Überprüfung!)
• d) ein Drittel der Fahrzeit mit 66 km/h, zwei Drittel mit 87 km/h zurückgelegt wird!(Hinweis: Kreative Aufgabenlösung vonnöten: entweder algebraisch über das Lösen von 2 Gleichungen mit 2 Unbekannten, oder graphisch mit rechnerischer Überprüfung der Lösung!)
  

Zeichnen Sie zu jeder Teilaufgabe auch ein Zeit-Ort-Diagramm! (100 km = 5 cm, 1 h = 4 cm)

Lösung

weiter zur nächsten Seite