Mechanics11/Seite3
Interpretation von Zeit-Orts-Diagrammen
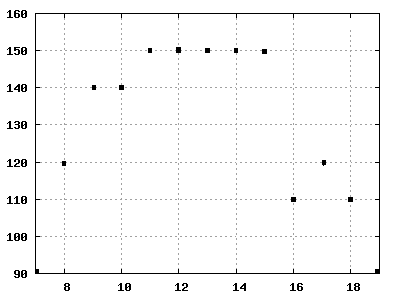
Aufgabe 1.5: Radltour
Desiree und Marc radeln zum Plansee. Sie fahren um 7.00 Uhr los und kommen um 19.00 wieder zuhause an.
Entlang der Straße sind Kilometersteine. Jede volle Stunde notieren sie ihre Position x .
Rechtswertachse: Uhrzeit in Stunden, Hochwertachse: Ortskoordinate in km
- a) Berechnen Sie für jedes Zeitintervall von 1 Stunde die durchschnittliche Geschwindigkeit! Benutzen Sie Berechnungsformeln!
- b) Beschreiben Sie für jedes Zeitintervall den Verlauf der Bewegung in Worten! Mögliche Interpretation?
- c) Berechnen Sie die Durchschnittsgeschwindigkeit für die ersten 4 Stunden! Wie lässt sich diese graphisch darstellen?
1. Bewegungsgleichung
Wir leiten eine allgemeine Gleichung für geradlinig-gleichförmige Bewegungen her:
aus
[math]v = \frac{\Delta x}{\Delta t} = \frac{x - x_0}{\Delta t}[/math]
folgt
x = x0 + v[math]\Delta t[/math]
Damit lässt sich z.B. bei bekanntem Anfangsort x und bekannter Geschwindigkeit v die aktuelle Position am Ende eines Zeitintervalls berechnen.
Nehmen wir für x0 den Ort x(0) zur Zeit t = 0, so ergibt sich die
1. Bewegungsgleichung:
x(t)= x0 + v t
Hierbei handelt es sich um eine lineare Gleichung. In der Mathematik schreiben wir immer
y(x) = t + mx
Dabei ist x die unabhängige, y die abhängige Variable. t ist der sog. y-Achsenabschnitt, m der Steigungsfaktor ("Steigung").
In der Bewegungsgleichung ist die unabhängige Variable die Zeit t, der Ort x hängt von ihr ab. Die Geschwindigkeit v ist die Steigung der Zeit-Ort-Geraden.
Aufgabe 1.6: Wettflug
Ein Bussard fliegt mit einem Falken um die Wette. Der Bussard bekommt 14 km Vorsprung vom Startpunkt aus gemessen, weil er mit 95 km/h deutlich langsamer ist als der Falke (153 km/h).
- a) Wann und wo holt der Falke den Bussard ein?
- b) Wer gewinnt den Wettflug bis zum Gipfelkreuz des Hörnle (40 km vom Start entfernt)?
- c) Zeichnen Sie ein geeignetes Zeit-Ort-Diagramm!