Astro13/3. KG

|

Newtonsches Gravitationsgesetz und Kreisbewegung

Eine Kreisbewegung kommt dadurch zustande, dass ein sich bewegender Körper eine konstante Kraft zum Drehzentrum hin erfährt, die sogenannte Zentralkraft. Sie lässt sich berechnen mit der Formel

Fz = m [math]\omega^2[/math] r

wobei m die Masse des Körpers, [math]\omega[/math] die Winkelgeschwindigkeit und r der Radius der Kreisbahn ist.

Dabei gilt

[math]\omega = \frac{2 \pi}{T}[/math]

T ist die Umlaufzeit des Körpers.

Beim Umlauf eines Planeten um die Sonne ist die Gravitationskraft die zentrale Kraft. Sie ist nach Isaac Newton umgekehrt proportional zum Quadrat des Abstandes vom Zentralkörper:

F_grav ~ [math] \frac{1}{r^2}[/math]

Außerdem ist F_grav

proportional zu den beiden sich gegenseitig anziehenden Massen M und m :

F_grav ~ M · m

Zusammen mit einer Proportionalitäskonstanten G ergibt sich das Newtonsche Gravitationsgesetz

Fgrav = [math]G \frac{M m}{r^2}[/math]

Bei einer Kreisbewegung eines leichten Körpers im Schwerefeld eines massereichen Körpers gilt also

F_z = F_grav

[math]m \omega^2 r[/math] = [math]G \frac{M m}{r^2}[/math]

und daraus

[math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G M} [/math]

Wir erkennen einen Zusammenhang zwischen der Umlaufzeit und dem Kreisradius - je weiter entfernt z.B. der Planet von der Sonne ist, umso größer die Umlaufzeit. Wir erkennen weiter, dass das Verhältnis [math]\frac{T^2}{r^3}[/math] lediglich von der Masse M des Zentralkörpers abhängt, als für alle Planeten, die um die Sonne kreisen, den gleichen Wert [math]\frac{4 \pi^2}{G M}[/math] besitzt.

Dies hatte Kepler schon in seinem 3. Keplerschen Gesetz erkannt.

Es folgt

[math]\frac{T_1^2}{r_1^3} = \frac{T_2^2}{r_2^3}[/math]

[math]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/math]

Ohne Beweis sei mitgeteilt, dass dieses Verhältnis auch für den allgemeineren Fall gilt, dass die Bahnen der umlaufenden Körper Ellipsen sind. Dann gilt mit a₁ und a₂ als großen Halbachsen

[math]\frac{T_1^2}{T_2^2} = \frac{a_1^3}{a_2^3}[/math]

3. Keplersches Gesetz

Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die Kuben ihrer großen Halbachsen.

A6. Saturn

Der Ringplanet Saturn durchläuft eine Ellipse mit der großen Halbachse a = 9,56 AE und der Exzentrizität [math]\varepsilon[/math] = 0,056 .

• a) Berechnen Sie den Aphel- und Perihelradius!
• b) Wie lange benötigt Saturn für einen Umlauf um die Sonne?

A7. Mars

Der erste äußere Planet, der Mars, umrundet die Sonne einmal in 687 Tagen.

• a) Berechnen Sie seine große Halbachse (in AE) !
• b) Berechnen Sie die Entfernung von der Erde während der Opposition!

A8. Pluto

Vor einigen Jahren wurde Pluto sein Status als Planet aberkannt, da er seine Umlaufbahn nicht ausreichend von interplanetarer Materie reinigen konnte. Er ist dazu zu klein. Wir rechnen ihn heute den Zwergplaneten zu.

Im Aphel seiner Bahn ist er 7423 km von der Sonne entfernt. Seine Geschwindigkeit dort beträgt 3,67 km/s . Ein Umlauf um die Sonne geschieht in 248 Jahren.

• a) Berechnen Sie die große Halbachse (in AE) und die Bahnexzentrizität!
• b) Wie weit ist Pluto im Perihel von der Sonne entfernt? Welche Geschwindigkeit hat er dort?

A9. Satelliten

Ein Fernsehsatellit soll fest über einem bestimmten Punkt der Erdoberfläche stehen ("geostationär").

• a) Warum ist dies nur über dem Erdäquator möglich? Fertigen Sie dazu eine maßstabsgetreue Skizze an! Zahlenwerte siehe c).
• b) Wie groß muss die Umlaufzeit T sein? Berechnen Sie die Winkelgeschwindigkeit [math]\omega[/math]!
• c) Berechnen Sie die Flughöhe über der Erdoberfläche! Tipp: Gehen Sie dabei von dem Ansatz aus, dass die Zentralkraft der Kreisbewegung die Gravitationskraft ist. (Ergebnis: 35873 km = 3,6 10⁴ km)
• d) Wie lange ist ein Funksignal vom Satelliten zur Erde unterwegs?

Zwei-Körper-Problem

Das Newtonsche Gravitationsgesetz ist symmetrisch in den beiden Massen M und m, was die physikalische Gesetzmäßigkeit beschreibt, dass sich beide Massen mit der gleichen Kraft gegenseitig anziehen, d. h. M zieht m genauso stark an wie m M anzieht. Warum sollte auch eine der beiden Massen ausgezeichnet sein? Dies ist besonders leicht dran zu erkennen, dass die beiden Massen auch gleich sein könnten, also M = m . Wer umkreist dann aber wen?

Dies ist in der Astrophysik bei Doppelsternsystemen bekannt. Richtig, sie umkreisen sich gegenseitig.

Wie kann das sein?

Zum Verständnis brauchen wir das Konzept des Massenschwerpunktes eines Systems von Massen: Hat man z. B. zwei Gewichte M und m , verbindet sie mit einer festen Stange, dann kann man die Stange am Schwerpunkt unterstützen und sie kippt nicht um.

Die Hebelwirkung der linken und rechten Seite ist gleich:

M r₁ = m r₂

(Die Stange wird als masselos betrachtet.)

Setzen wir die Stange in Drehung, so lässt sie sich am Schwerpunkt auf dem Finger balancieren.

Zwei Massen im Weltraum verhalten sich genauso, sie umkreisen beide den Schwerpunkt, mit der gleichen Frequenz.

Ohne Beweis sei mitgeteilt, dass sich dann die Gleichung

[math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G M} [/math]

verändert zu

[math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G (M + m)} [/math]

und, im allgemeinen Fall, beide Körper (zueinander ähnliche) Ellipsen um den Schwerpunkt durchlaufen.

Zwei Körper bewegen sich durch gegenseitige Anziehung umeinander

Auch die relative Bewegung von M um m bzw. von m um M ist wieder eine Ellipse mit der Halbachse a .

Für diese gilt allgemein:

[math] \frac{T^2}{a^3} = \frac{4 \pi^2}{G (M + m)} [/math]

Wir erkennen an dieser Gleichung, dass das 3. KG eine Näherung ist, die nur für im Vergleich zur Sonne sehr kleine Planetenmassen gilt. (Dies ist hinreichend erfüllt. Berechnen Sie dazu, wie viel Prozent der Sonnenmasse etwa der massenreichste Planet, der Jupiter, besitzt.)

A10. La Luna

Die Möndin bewegt sich auf einer annähernd kreisförmigen Ellipse um die Erde.
Hinweis: Schlagen Sie alle benötigten Größen in der Formelsammlung (siehe T6) nach!

• a) Das System Erde-Mond besitzt einen Schwerpunkt SP. Berechnen Sie die Entfernung r des Schwerpunkts vom Erdmittelpunkt!
• b) Berechnen Sie die Dauer eines Umlaufs um den Schwerpunkt in Tagen („siderischer“ Monat) ! Ergebnis: 27,3 d .
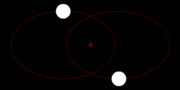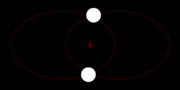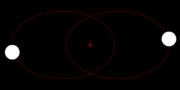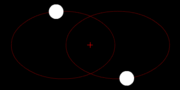
• c) Erklären Sie anhand einer übersichtlichen Skizze, weshalb zwischen zwei Neumondstellungen eine längere Zeitspanne liegt ( 29,5 d , „synodischer“ Monat)! Hinweis: Bei Neumond liegt der Mond zwischen Sonne und Erde!
• d) Erklären Sie, weshalb ein Monat 28 – 31 Tage dauert!

Bestimmung der Astronomischen Einheit AE

Es war eine große Herausforderung an die Astronomie, den exakten Zahlenwert für die Astronomische Einheit zu bestimmen. Zunächst werteten Astronomen auf der ganzen Welt die seltenen Venusdurchgänge vor der Sonne trigonometrisch aus, erreichten damit aber keine sehr große Genauigkeit.

Heute lässt sich mittels eines Radarsignals die Entfernung zur Venus direkt messen, und dann können wir aus dem 3. KG den Absolutwert der Astronomischen Einheit berechnen:

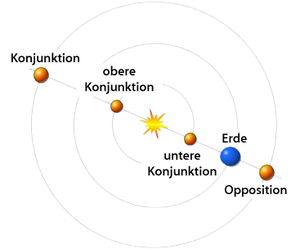
Ist d die kürzeste Entfernung der Venus von der Erde (wird erreicht in der unteren Konjunktion), a₁ die große Halbachse der Venusbahn, T₁ die Umlaufzeit der Venus um die Sonne, so gilt nach Kepler 3 im Vergleich mit der Erde

[math]\frac{a_1^3}{a^3} = \frac{T_1^2}{T^2} [/math]

Setzen wir

a₁ = a - d

darin ein, so erhalten wir nach einigen Umformungen den Ausdruck

[math]a = \frac{d}{1 - (\frac{T_1}{T})^\frac{2}{3}}[/math]

A11. Astronomische Einheit

• a) Leiten Sie die obige Formel zur Berechnung der großen Halbachse der Erde (1 AE) aus dem 3. KG ab!
• b) Steht die Venus in unterer Konjunktion zur Erde, beträgt die Laufzeit eines Radarsignals zum Planeten und zurück insgesamt 273,3 Sekunden. Berechnen Sie daraus die minimale Entfernung Erde - Venus!
• c) Berechnen Sie mit obiger Formel den Zahlenwert der Astronomischen Einheit in km und in m !
• d) Vergleichen Sie mit dem offiziell festgelegten Wert 1 AE = 149 597 870 km !
• e) Merken Sie sich den Zahlenwert 1 AE = 150 Millionen km als gute Näherung.

|