Astro13/Raumfahrt
Contents
Interplanetare Raumfahrt
Hubarbeit im Gravitationsfeld
Einen Flugkörper zu einem weit von der Erde entfernten Himmelskörper zu schicken ist vor allem eine energetische Frage. Wie lässt sich der Bedarf an Treibstoff minimieren?
Gehen wir zunächst von der Arbeit aus, ein Raumfahrzeug im Gravitationsfeld der Erde von der Oberfläche aus anzuheben. Leider gilt die bequeme Formel
WH = m g h
nur in unmittelbarer Nähe der Oberfläche, denn sie enthält den Ortsfaktor g , der vom Ort abhängt. Wir wissen bereits, dass weiter draußen die Gravitation nach dem Newtonschen Gravitationsgesetz abnimmt:
Fgrav = [math]G \frac{M m}{r^2}[/math]
Die Übereinstimmung beider Beziehungen an der Erdoberfläche eröffnet eine elegante Möglichkeit, die Masse der Erde zu berechnen (siehe Aufgabe A....)!
Wie berechnen wir also die Hubarbeit für große Höhen?
Mitteilung: Eine Integration der Gravitationskraft über die Hubhöhe ergibt den Ausdruck
[math]W_H = G M m ( \frac{1}{r_1} - \frac{1}{r_2} )[/math]
wobei r1 der Anfangs- und r2 der Endradius ist. M ist die Masse der Erde, m die Masse des gehobenen Körpers.
Wir erkennen, dass für r2 > r1 der Ausdruck für WH positiv wird, was besagt, dass Arbeit aufgewandt werden muss.
Wird das Raumschiff von der Erdoberfläche ins Unendliche gehoben, heißt das r2 wird unendlich, und damit
[math]W_H = G M \frac{m}{R}[/math]
wobei R der Erdradius ist.
A12. Masse der Erde, Masse der Sonne
- a) Berechnen Sie die Masse der Erde mit Hilfe des Ortsfaktors g und dem Newtonschen Gravitationsgesetz, ausgewertet an der Erdoberfläche!
- b) Berechnen Sie die Masse der Sonne aus den Umlaufdaten der Erde, mit Hilfe des Zahlenwerts für die Astronomische Einheit!
- c) Ermitteln Sie das Massenverhältnis von Erde und Sonne!
- d) Wo befindet sich der Massenschwerpunkt des Systems Erde-Sonne?
A13. Masse des Jupiters
Die Masse des Jupiters lässt sich schon aus den Daten ermitteln, die die Beobachtung mit einem kleinen Fernrohr liefert:
Wir sehen den Planeten als kleines Scheibchen, auf dem sogar die Wolken längs des Äquators erkennbar sind. In Oppositionsstellung hat es einen Winkeldurchmesser von 0,013° .
- a) Berechnen Sie den Durchmesser des Planeten in km ! Hinweis: Bei so kleinen Winkeln dürfen Sie die entsprechende Bogenlänge als Näherungswert benutzen. Sowohl die Jupiterbahn als auch die Erdbahn ist mit guter Näherung kreisförmig.
- b) Die 4 großen Jupitermonde (Io, Europa, Ganymed und Kallisto) sind als hübsche "Perlenkette" um den Planeten aufgereiht. Der Mond Kallisto benötigt für eine volle Umkreisung des Planeten 16,7 Tage. In Opposition beträgt der maximale Winkelabstand zwischen Kallisto und der Mitte des Jupiterscheibchens 0,17° . Berechnen Sie den Kreisbahnradius von Kallisto!
- c) Berechnen Sie daraus die Masse des Jupiters!
http://wdrblog.de/teleskop/jupiter_monde_400q.jpg
Fluchtgeschwindigkeit
In seinem berühmten Roman "Von der Erde zum Mond" von 1865 beschreibt Jules Verne, wie eine bemannte Raumkapsel mit einer Kanone zum Mond geschossen wird. Die Geschwindigkeit, mit der das Projektil das Kanonenrohr verlassen müsste, nennen wir die Fluchtgeschwindigkeit. Genauer ist es die kleinste Geschwindigkeit, um die Erde auf Nimmerwiedersehen zu verlassen.
Wir ermitteln sie aus dem Energieansatz
Ekin = Epot
[math]\frac{1}{2} m v^2 = G M \frac{m}{R}[/math]
Und erhalten
[math]v_F = \sqrt{\frac{2 G M}{R}}[/math]
A14. Einschlag
- a) Berechnen Sie die Fluchtgeschwindigkeit von der Erd- und Mondoberfläche!
- b) Stellen Sie eine Vermutung auf, weshalb um die Erde eine Atmosphäre existieren kann, nicht aber um den Mond! Hinweis: Denken Sie an die kinetische Gastheorie!
- c) Wie groß ist die Einschlaggeschwindigkeit eines Meteoriten auf der Erde bzw. dem Mond mindestens? Hinweis: Es darf davon ausgegangen werden, dass der Meteorit aus dem Unendlichen ohne wesentliche Abbremsung in der Atmosphäre herabstürzt.
Hohmann-Bahn
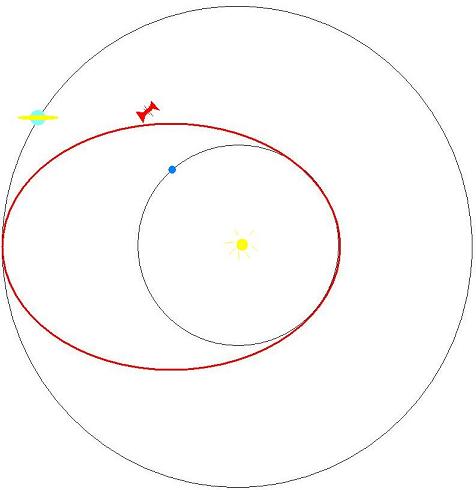
Hat sich eine Raumsonde ein gutes Stück von der Erde entfernt, kreist sie mehr oder minder auf der Umlaufbahn der Erde um die Sonne. Wenn wir nun einen äußeren Planeten erreichen wollen, etwa den Saturn, muss das Raumfahrzeug beschleunigt werden, so dass es die Perihelgeschwindigkeit einer Ellipse erreicht, deren Aphel auf der Bahn des Saturn liegt. Beachten Sie, dass die Sonne im Brennpunkt dieser Ellipse steht!
Eine solche Bahn ist energetisch am Günstigsten, auch wenn in der Raumfahrtpraxis oft Spiralbahnen bevorzugt werden. Wir nennen sie die Hohmann-Bahn von der Erde zum Saturn.
Sehen Sie sich dazu auch im Internet die Simulation eines Fluges zum Jupiter an.
Wenn wir die Fluggeschwindigkeit an einem beliebigen Ort der Bahn berechnen wollen, so können wir die Formel
[math]v = \sqrt{G M ( \frac{2}{r} - \frac{1}{a} ) }[/math]
benutzen, die Sie auch in der Formelsammlung finden. (Ohne Beweis.)
r ist dabei die momentane Entfernung von der Sonne, und a die große Halbachse der Ellipse.
Insbesondere ist damit die Perihel- und Aphelgeschwindigkeit berechenbar.
Zeigen Sie: Für a = r ergibt sich die Bahngeschwindigkeit einer Kreisbahn, und für a gegen unendlich die Fluchtgeschwindigkeit.
A15. Rundum-Wurf
Rufen Sie die Simulation eines waagrechten Wurfs von einem hohen Turm von Peter Brichzin, Michaeli-Gymnasium München, auf. Die Höhe des Turms betrage 2000 km , jegliche Luftreibung darf vernachlässigt werden.
Simulieren Sie die folgenden Fälle und berechnen Sie die Antworten auf folgende Fragen:
- a) Wie groß ist die Aufschlag-Geschwindigkeit eines Steins auf dem Erdboden bei geringer Abwurf-Geschwindigkeit?
- b) Wie schnell muss der Stein abgeworfen werden, damit er die Erde auf einer Kreisbahn umrundet?
- c) Wie groß muss die Abwurfgeschwindigkeit sein, dass der Stein auf einer Hohmann-Bahn zum Mond fliegt?
- d) Ab welcher Geschwindigkeit kehrt der Stein nicht mehr zurück?