User:Max.DM11

Hi my name is Max and i`m a pupil at the Gisela-Gymnasium.[1]

Sandbox

Elastischer Stoß Versuch

2 Wägen mit entgegengesetzten Geschwindigkeiten treffen sich elastisch. Beide haben unterschiedliche Masse und Geschwindigkeit.
Frage: Was passiert nach dem crash?
Wagen A: M_a = 0,1 kg V_a = 0,4 [math]\frac {m}{s}[/math]
Wagen B: M_b = 0,9 kg V_b = 0,1 [math]\frac {m}{s}[/math]


Lsg:
Wagen B bleibt stehen.
Wagen A wird mit -0,5 [math]\frac {m}{s}[/math] zurückgestoßen.

1.6 Wettflug

Ein Bussard fliegt mit einem Falken um die Wette. Der Bussard bekommt 14 km Vorsprung vom Startpunkt aus gemessen, weil er mit 95 km/h deutlich langsamer ist als der Falke (153 km/h).

   * a) Wann und wo holt der Falke den Bussard ein?
   * b) Wer gewinnt den Wettflug bis zum Gipfelkreuz des Hörnle (40km vom Start entfernt)

[math]V_B= 95 \frac {km} {h} [/math]

[math]V_F = 153 \frac {km} {h}[/math]

Der Bussard hat 14 km Vorsprung.
a)
[math]x(t) = 0km + 153 \frac {km} {h} * \Delta t[/math]

[math]x(t) = 14km + 95 \frac {km} {h} * \Delta t[/math]

[math]153 \frac {km} {h} * \Delta t = 14km + 95 \frac {km} {h} * \Delta t[/math]
[math]58 \frac {km} {h} * t = 14km[/math]

t = 0,24h = 14 min
b) Der Falke gewinnt da er den Bussard nach 14min überholt obwohl er Vorsprung hat.
Am Gipfel vom Hörnle essen dann beide nach dem Rat von unserem Lehrer Kässpätzle.

--Max.DM11 09:50, 9 October 2008 (UTC)

Aufgabe 4.7

a) E=[math]\frac {1}{2}[/math]mv²
-->[math]\frac {1}{2}[/math]*2000kg*50[math]\frac {km}{h}[/math]=193kJ
b) E=mgh
-->1000kg*9.61[math]\frac {n}{kg}[/math]*200m=1,96MJ
c) E=[math]\frac {1}{2}[/math]mv²
-->[math]\frac {1}{2}[/math]*4000t*1[math]\frac {m}{s}[/math]="MJ

Geisterfahrer

Ein Geisterfahrer fährt mit konstanter Geschwindigkeit(120 km/h) auf einer Landstraße. Auf der gleichen Spur fährt in normaler Richtung ein 40-Tonner mit konstanter Geschwindigkeit(80 km/h).
Sie sind 20 km voneinander entfernt.
a) Zeichne ein qualitatives x/t Diagramm
b) wann treffen sie sich?
c) Was ist die relative Aufschlagsgeschwindigkeit?

von User:ManuM11, User:Max.DM11, User:Atheist^^m11

Lösung:
b)[math]\Delta{x}[/math] = 20km
v_gesamt = 120km/h + 80km/h = 200km/h
t = [math]\frac{x}{v}[/math] = [math]\frac{20 km}{200 km/h}[/math] = 0,1h = 6 Minuten
c) 120km/h + 80km/h = 200km/h

Anfahren!

Eine Lokomotive fährt aus dem Stillstand mit der konstanter Beschleunigung a = 0,850 m/s² an.

    a) Nach welcher Zeit hat sie die Geschwindigkeit v = 75,0 km/h erreicht?

[math]a= 0,850 \frac {m} {s^2} [/math]

Ges: Nach welche Zeit gilt: [math]v= 75,0 \frac {km} {h} [/math]
Lsg: [math]a= \frac {\Delta v} {\Delta t} [/math]

[math]\Delta t= \frac {\Delta v} {a} = \frac {75 km/h} {0,850 m/s^2} = \frac {20,83m/s} {0,850 m/s^2} = 24,5 s [/math]

Von Null auf Hundert

Die Testfahrt eines neuen Motorrads ergab eine Geschwindigkeitszunahme von 0 auf 100 km/h in 3,87 s.

    a) Berechnen sie die mittlere Beschleunigung und den bei dieser Beschleunigung
       in dieser Zeit zurückgelegten Weg!

t= 3,87s
v(t)=a*t

[math]x(t)= \frac {v(t)} {t} = \frac {27,78 m/s} {3,87s} = 7,12 \frac {m} {s^2} [/math]
[math]x(t)= \frac {1} {2} *7,12 \frac {m} {s^2}*(3,87s)^2= 53,75m [/math]

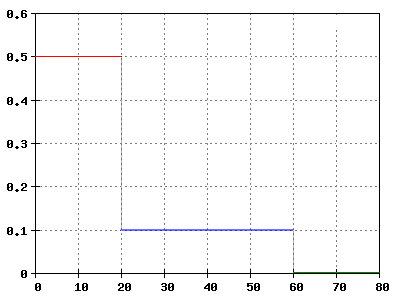
Zugfahrt

Rechtswert: Zeit t in s
Hochwert: Beschleunigung a in m/s²

Ein Zug fährt an. Die Abhängigkeit seiner mittleren Beschleunigung von der Zeit gibt das Diagramm wieder.

• a) Berechnen Sie die Geschwindigkeiten, die der Zug nach 20 s, 60 s und 80 s hat, und zeichnen Sie das t-v-Diagramm!
• b) Berechnen Sie mithilfe des t-v-Diagramms den zurückgelegten Weg für die gleichen Zeitpunkte und zeichnen Sie das t-x-Diagramm!

Lösung: a)

[math]v(t)_1= a_1*t_1= 0,5 \frac {m} {s^2}*20s= 10 \frac {m} {s} [/math]

[math]\Delta v(t)_2= a_2*\Delta t_2= 0,1 \frac {m} {s^2}*40s= 4 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

[math]\Delta v(t)_3= a_3*\Delta t_3= 0 \frac {m} {s^2}*40s= 0 \frac {m} {s} =\gt v= 14 \frac {km} {h} [/math]

Gewehrkugel

Die Kugel eines Gewehrs soll im Lauf gleichmäßig beschleunigt werden.

• a) Nach welcher Zeit verlässt die Kugel den Lauf ?
• b) Wie groß ist die Beschleunigung, wenn der 80 cm lange Lauf mit 760 m/s verlassen wird ?

Lösung:
a)

[math] x(t)= \frac {1}{2}a*t^2 =\gt t= 2 \frac {x(t)} {v}= 2\frac {0,8m} {760m/s}= \frac {21} {10000} s[/math]
b)

[math] a= \frac {\Delta v} {\Delta t} =\gt a= \frac {760 m/s} {\frac {21} {10000} s}= 361000 \frac {m} {s^2}[/math]

Kavaliersstart

Beim Anfahren eines Wagens nimmt man folgende Meßreihe auf :

Zeit t in s	Ort x in m
0	0
1	0,5
2	2
3	4,5
4	8
4,2	8,8
5	12
6	16
7	20

• a) Mit welchen Weg-Zeit-Funktionen lassen sich die Bewegungen in den Zeitab­schnitten 0 < t < 4 s und 4 s < t < 7 s beschreiben?
• b) Bestimmen Sie die Beschleunigung und die Momentangeschwindigkeit für jeden Punkt der Tabel­le! Zeichnen Sie das v(t)-Diagramm! Bestimmen Sie daraus mit Hilfe der Fläche den Ort x(6,5 s) zu t = 6,5 s!
  

Aufgabe 4.6: Enegievergleich

    Berechnen Sie die Energie
         a) eines Kleinbusses von 2.0 t Masse bei einer Geschwindigkeit von 50 km/h.
         b) von 1,0 m³ Wasser in einer Höhe von 200m ( Walchenseekraftwerk )
         c) von 4000 m³ Wasser im Rhein, wenn die Fließgeschwindigkeit 1,0 m/s beträgt!
    Welche Art von Energie liegt jeweils vor?

a) m= 2,0t; v= 50km/h

[math] E_k = 0,5 m*v^2 = 0,5*2000kg*13,9= 192,9kJ [/math]

b) [math]V= 1,0m^3; h= 200m[/math]
[math]=\gt m= 1000kg[/math]
[math]E_H= m*g*h= 1000[/math]kg[math]*9,81 N/[/math]kg[math]*200m= 1962000J= 1962kJ[/math]
c) [math]V= 4000m^3; v= 1,0 m/s; m= 4000000kg= 4000t[/math]

[math]E_K= 0,5mv^2= 0,5*4000000kg*1^2= 2000kJ= 2,0MJ[/math]

5.7

A)

v = g * r = 3,1 [math]\frac{m}{s}[/math]

B)

E_pot = E_kin

m * g * h = [math]\frac{1}{2}[/math] * m * v² - [math]\frac{1}{2}[/math] * m * v₀²

g * 2 * r = [math]\frac{1}{2}[/math] * (v² - v₀²)

4 * g * r = v² - v₀²

v² = v₀² + 4 * g * r = (3,1² + 4 * 9,81 * 1,0) ([math]\frac{m}{s}[/math])²

=> v = 7,0 [math]\frac{m}{s}[/math]

C)

h = [math]\frac{v_2}{2*g}[/math] = (3,1)²/(2*9,81) = 0,5m

Die Dose wird 1.5 hochgeworfen.

5.9

m = 0.80 kg

r = 0,50 m

v = 3,4 [math]\frac{m}{s}[/math]

F_Z = m * [math]\frac{v^2}{r}[/math]

tan α = [math]\frac{F_Z}{F_G}[/math] = [math]\frac{(m * \frac{v^2}{r})}{(m * g)}[/math] = [math]\frac{v^2}{r*g}[/math] = [math]\frac{\frac{40}{3,6}^2}{20*9.81}[/math] = 0,629

=> α = 32°