User:ManuM11
Hello, my name is Manuel and I attend the 11th grade of Gisela-Gymnasium in Munich.
Contents
Sandbox
geg:
VB = 95[math]\frac{km}{h}[/math]
VF = 153[math]\frac{km}{h}[/math]
XB=14km
ges:
Treffpunkt
Lsg:
t = [math]\frac{Xb}{\Delta{V}}[/math] = [math]\frac{14km}{58\frac{km}{h}}[/math] = 14 min
2.6 Anfahren
geg: a = 0,850 m/s² v = 75 km/h
ges: t
Lsg: v(t) = a * t
[math]\frac{v(t)}{a}[/math] = t = [math]\frac{20,8m/s}{0,850m/s^2}[/math] = 24,47s
t = 24,5s
Geisterfahrer
Ein Geisterfahrer fährt mit konstanter Geschwindigkeit(120 km/h) auf einer Landstraße.
Auf der gleichen Spur fährt in normaler Richtung ein 40-Tonner mit konstanter Geschwindigkeit(80 km/h).
Sie sind 20 km voneinander entfernt.
a) Zeichne ein qualitatives x/t Diagramm
b) wann treffen sie sich?
c) Was ist die relative Aufschlagsgeschwindigkeit?
von User:ManuM11, User:Max.DM11, User:Atheist^^m11
b)[math]\Delta{x}[/math] = 20km
vgesamt = 120km/h + 80km/h = 200km/h
2.7 Von Null auf Hundert
Die Testfahrt eines neuen Motorrads ergab eine Geschwindigkeitszunahme von 0 auf 100 km/h in 3,87 s.
a) Berechnen sie die mittlere Beschleunigung und den bei dieser Beschleunigung
in dieser Zeit zurückgelegten Weg!
t= 3,87s
v(t)=a*t
[math]a= \frac {v} {t} = \frac {27,78 m/s} {3,87s} = 7,12 \frac {m} {s^2} [/math]
[math]x(t)= \frac {1} {2} *7,12 \frac {m} {s^2}*(3,87s)^2= 53,75m [/math]
2.8 Zugfahrt
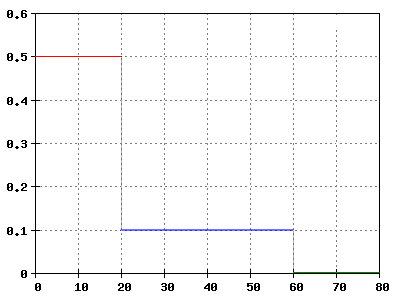
Rechtswert: Zeit t in s Hochwert: Beschleunigung a in m/s2
Ein Zug fährt an. Die Abhängigkeit einer mittleren Beschleunigung gibt das Diagramm wieder.
a) Berechnen Sie die Geschwindigkeiten, die der Zug nach 20s, 60s und 80s hat, und
zeichnen Sie das t-v Diagramm!
Aufgabe 3.10: Landetraining
Ein Fallschirmspringer kommt mit einer Geschwindigkeit von 7,5 m/s auf den Boden auf.
Zum Training springt er zunächst von einer Plattform. Wie hoch muss diese sein, damit
er mit der gleichen Geschwindkeit aufkommt?
[math]t= 7.5 \frac {m} {s}[/math]
[math]v=a*t[/math]
[math] t= \frac {v}{a} = \frac {7,5}{9.81}s = 0,764s[/math]
[math] h = \frac {1}{2}g*t^2 = \frac {1} {2}*0,764^2*9,81=2.81m[/math]
Aufgabe 3.11: Verweis!
Eine Schülerin des Gisela-Gymnasium lässt einen Schneeball aus dem 3. Stock
(Stockwerkshöhe 3,45m) in den Schulhof fallen.
a) Wie lang ist die Fallzeit?
b) Mit welcher Geschwindigkeit kommt er unten an?
c) Berechnen Sie Fallzeit und Endgeschwindigkeit für einen Fall aus der
gleichen Höhe auf dem Mond! (Dort ist die Gravitationsfeldstärke nur
1/7 so groß wie auf der Erde.)
a) h= 4*3,45m
[math]t= \sqrt {\frac {2h} {g}} = 1,67s[/math]
b) [math]v^2=2gh[/math]
[math]v=\sqrt {\frac {2h} {g}}=16,4 \frac {m}{s}= 59 \frac {km} {h}[/math]
c) [math] v'= \sqrt {2*1/7*g*h}=6,2 \frac {m} {s} [/math]
[math]t'=4,4s[/math]
Aufgabe 4.7: Hell Racer
Ein Spielzeugauto der Masse 70g fährt auf einer horizontalen Bahn mit der konstanten Geschwindigkeit 5,0 m/s.
Anschließend durchfährt es einen senkrechten Halbkreis mit Radius 50cm.
Die Reibung darf vernachlässigt werden.
a)Mit welcher kinetischer Energie und mit welcher Geschwindigkeit verlässt das Auto den Halbkreis?
b)Mit welcher Geschwindigkeit erreicht es wieder die horizontale Bahn?
c)Das selbe Auto wird mit 5,0 m/s senkrecht nach oben geworfen. Welche Geschwindigkeit besitzt es in 1,0 m Höhe?
a)
EHöhe[math] = mgh = 0,007kg * 9,81\frac {N}{kg} * 1m = 0,69 J[/math]
Ekin1[math] = \frac{1}{2}mv^2 = 0,875 J[/math]
Ekin2 = Ekin1 - EH = 0,19 J
b) [math]v= \sqrt {\frac {2E} {m} } = 2,33 \frac {m} {s} [/math]
c) [math]v= 5,0 \frac {m} {s} h=1,0m[/math]
[math]x(t)= \frac {1} {2}a*t^2[/math]
[math]t= 0,45s[/math]
[math]v=[/math]v0[math]-g*t= 0,57 \frac {m} {s}[/math]
5.4 Luftkampf
Selbst ein trainierter Pilot eines Kampfjets überlebt bestenfalls Beschleunigungen von der Größe der zehnfachen Fallbeschleunigung. Mit welcher Geschwindigkeit kann er höchstens eine Kurve vom Radius 2,0 km durchfliegen?
r = 2000m
a = 10*9.81m/s² = 98.1m/s²
a = w²*r => w = [math]\sqrt{\frac{a}{r}}[/math] = 0,22 1/s
v = r * w = 2000m * 0,22 1/s = 442,9 m/s = 1595 km/h