Carnot Principle - motivation and examples
| Thermodynamics | |
|---|---|
| Introduction | What is this thing called Thermodynamics??? | Definitions | Thermal Equilibrium and Zeroth Law | Limitations |
| First Law | Work, Heat, Energy, and the First Law | Work, Heat, Energy, and the First Law (simplied) | Derivatives | Derivatives Exercise | Reversibility, Enthalpy, and Heat Capacity |
| Second Law | Things to Think About | Observations and Second Law of Thermodynamics | Alternative Approach - the Clausis Inequality | Consequences of the Second Law | Consequences of the Second Law (simplified) | Carnot Principle - motivation and examples | Equivalence of Second Law Statements* |
| Third Law | Third Law of Thermodynamics | Consequences of Third Law* |
| Development of Thermodynamics | The Thermodynamic Network | Network Exercise | Equations of State (EOS) | EOS Example, Reading Tables, and Numerical Analysis | EOS Exercises | Thermochemistry |
* Optional Section | |
| This section demonstrates the use of the Carnot cycle. First it proves the Carnot principle. Then it uses the Carnot cycle to evaluate a cycle problem. |
Contents
Carnot Principle - proof
Review
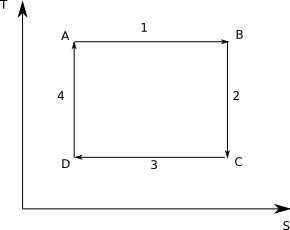
To review a Carnot cycle is a theoretical heat engine composed of four steps:
- Reversible, isothermal expansion of a gas
- Reversible, adiabatic expansion - cooling the gas
- Reversible, isothermal compression
- Reversible, adiabatic compression, returning the gas to its original state
Graphical it looks like:
Note that by the second law that the adiabatic steps have constant entropy and hence are shown by vertical lines.
Carnot Efficiency
For the first step AB the heat is given by the Clausis inequality: [math]Q_{AB}=T_1(S_A-S_B)=T_1\Delta S[/math]
For the adiabatic steps, [math]Q=0[/math]
For the third step CD, [math]Q_{CD}=T_2(S_D-S_C)=-T_2\Delta S[/math]
The total heat removed is: [math]Q=Q_{AB}+Q_{CD}=T_1\Delta S-T_2\Delta S=(T_1-T_2)\Delta S[/math]
Since the cycle begins and ends in the same state, ΔU = 0.
Then from the first law:
[math]\begin{align} \Delta U & = Q+W = 0 \\ -W & = Q \\ & = (T_1-T_2)\Delta S \end{align}[/math]
Then the efficiency is
[math]\begin{align} \eta & = \frac{-W}{Q_{in}} \\ & = \frac{-W}{Q_{AB}} \\ & = \frac{(T_1-T_2)\Delta S}{T_1\Delta S} \\ & = \frac{T_1-T_2}{T_1} \end{align}[/math]
Which is the result we had before.
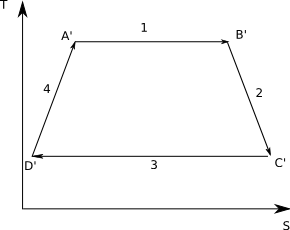
A Real Cycle
In a real cycle the Clausis inequality says that for the adiabatic steps we must Q > 0, since no real system is irreversible. Then the graph looks like:
From the diagram you can see that the magnitude of QC'D' is bigger than the magnitude of QCD. But both numbers are negative therefore
[math]Q_{C'D'} \lt Q_{CD}[/math]
(for example, -5 < -2)
Then,
[math]-W'=Q_{AB}+Q_{C'D'} \lt Q_{AB}+Q_{CD}[/math]
[math]\Rightarrow -W'\lt-W[/math]
[math]\Rightarrow\eta'\lt\eta[/math]
Hence, a real cycle cannot be as efficient as a Carnot cycle operating between the same temperatures. We have then proved the Carnot principle.
Example: Heat Engine
As an example of using the concept of efficiency to calculate work and heat, consider the following problem:
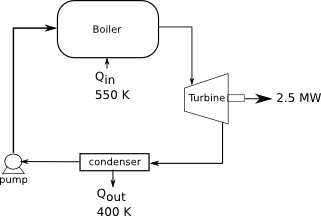
A power plant works at a boiler temperature of 550 K and an exhaust temperature of 400 K. If the efficiency is 75% of the Carnot cycle efficiency, how much heat is needed from fuel and how much is expelled through the exhaust, if the power output is 2.5 MW?
Hints:
- For a cycle problem always start with a diagram, placing given information on the diagram. While, this may not be necessary for simple problems, using it now will help you when you get to more complex problems.
- Remember that for any cycle ΔU=0.
- Be careful with signs.
Solution
Diagram:
Notes:
- In this problem we are given power output instead of work output. Since power is work per unit time, we will simply use power units instead of energy units (that is, Watts instead of Joules).
- As is typical, the given output is the net work. Some work is used to drive the pump, usually this is done by directly taking off part of the turbine output.
Given: net power output, temperatures of heat sources, efficiency (as percent Carnot efficiency).
Find: heat input, heat output.
[math]T_H=550 K[/math]
[math]T_C=400 K[/math]
[math]W=-2.5 MW[/math]
[math]\eta_{Carnot}=\frac{550-400}{550}=0.273[/math]
[math]\eta=0.75\eta_{Carnot}=(0.75)(0.273)=0.205[/math]
[math]W = -2.5 MW[/math]
[math]\eta=\frac{-W}{Q_{in}}\Rightarrow 0.205=\frac{2.5MW}{Q_{in}}[/math]
[math]\Rightarrow Q_{in}=12.2 MW[/math]
[math]\Delta U = 0 = Q + W = Q_{in}+Q_{out}+W[/math]
[math]12.2+Q_{out}-2.5=0[/math]
[math]\Rightarrow Q_{out} = -9.7 MW[/math]
Example: Refrigeration
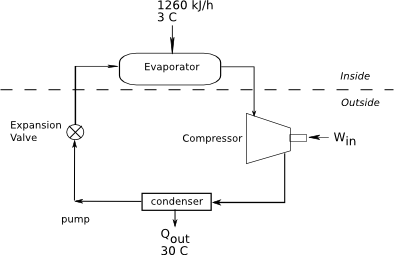
A refrigerator cycle with a COP of 2.7 is used to maintain the food compartment at 3 °C. The compartment continuously receives 1260 kJ/h of heat from the environment. The cost of electricity is 0.165 US$/kWh, and the refrigerator motor runs one-third of the time. Determine (a) the shaft power, in kW, the cycle requires, (b) the cost of the operating unit in dollars per day, (c) what is the rate of heat rejected to the outside, and (d) the maximum COP if the outside temperature is 30 °C.
Notes:
- Shaft power is the power provided by the motor, so-called because it is transferred by a turning a shaft.
- Reminder that we always use absolute temperature in thermodynamic calculations.
Solution
Diagram:
Given: COP, TC, TH, Qin, cost per kWh, refrigerator runs one-third of the time.
Find: Wnet, cost per day, Qin, COPCarnot.
(a) [math]COP=\frac{Q_{in}}{W_{net}}=2.7[/math]
[math]Q_{in}=1260 kJ/h[/math]
[math]W_{net}=\frac{1260\,kJ/h}{2.7}=\frac{467 kJ}{h}\,X\,\frac{h}{3600s}=0.13\,kW[/math]
(b) [math]cost\ per\ day = 0.13\ kW\,X\,\frac{$0.165}{kWh}\,X\,\frac{24h}{day}\,X\,\frac{1}{3} = $0.17 per\ day[/math]
(c) [math]\Delta U = 0 = Q_{in} + Q_{out} + W_{net} = 1260 kJ/h + Q_{out} + 467 kJ/h[/math]
[math]\Rightarrow Q_{out} = -1727 kJ/h[/math]
(d) [math]COP_{max}=\frac{T_C}{T_H-T_C}=\frac{276 K}{303 K - 276 K}=10.2[/math]
Exercises
Often cycles are combined. These two exercises are examples of this.
Hint: Draw a diagram! (Here it really does help)
Exercise 1
In this exercise we have two heat engines in series. In other words, the heat output from the first cycle is used as the heat input for the second.
Two Carnot heat engines operate in series. Engine A receives 2500 kJ of heat at 1000 K. All of the heat tranfser from engine A is used as energy input to engine B. This transfer occurs at 460 K. The heat rejected from engine B is 590 kJ. Find: (a) The amount of heat transferred between the two engines, (b) the total work output, (c) the efficiency of engine B, and (d) the temperature of the rejected heat from engine B.
Exercise 2
In this exercise the work produced by a heat engine is used to drive a refrigerator.
A Carnot heat engine operates between supply and rejection temperatures of 600 and 40 °C. Part of the work output of the heat engine is used to drive a Carnot refrigerator which operates between boundary temperatures of 40 and -20 °C. The heat input to the engine is 2100 kJ and the net work out (engine work minus refrigerator work) is 370 kJ. Determine the heat transfer to the refrigerator at -20 °C and the net heat transfer at 40 °C.