Mechanics11/Seite5
Contents
Bewegungen mit konstanter Beschleunigung
Versuch 2.1: Beschleunigung eines Wagens auf der schiefen Ebene
Wir verwenden den selben Versuchsaufbau wie im Versuch 1.1, nur dass diesmal die Ebene, auf der der Wagen hinab rollt, noch stärker geneigt ist. Wir nennen dies eine schiefe Ebene. Jetzt wird nicht nur die Reibung ausgeglichen, sondern der Wagen wird auch immer schneller. Es entsteht eine beschleunigte Bewegung.
Teststreifen einer Bewegung auf der schiefen Ebene, Spur (A)
Betrachten Sie den Teststreifen, den die Nadel beschrieben hat. Woran erkennen Sie, dass die Geschwindigkeit im Lauf der Zeit größer wird?
Aufgabe 2.1: Auswertung des Versuchs 2.1
Bestimmen Sie die Momentangeschwindigkeit des Wagens zu den Zeitpunkten t = 0,1 s , 0,2 s , 0,3 s … und stellen Sie die Ergebnisse in einer Tabelle zusammen! Benutzen Sie dazu immer zwei benachbarte Nadelstiche!
Das karierte Papier hat eine Kästchenbreite von 0,50 cm .
Achtung: Die Zeitdauer zwischen zwei Stichen beträgt nur 1/50 s = 0,02 s , nicht 1/100 s wie in Versuch 1.1, da der Elektromagnet mit einer Frequenz von 50 Hz arbeitet.
Fertigen Sie nun ein sauberes t-v-Diagramm der Bewegung! Überlegen Sie zunächst die Größe der Achsen und ihre Beschriftung!
Aufgabe 2.2: Versuch 2.1 mit einer anderen Neigung
Werten Sie nun entsprechend zu Aufgabe 2.1 diesen zweiten Teststreifen aus! Ist die Beschleunigung diesmal größer oder kleiner?
(Teststreifen einer Bewegung auf einer anders geneigten schiefen Ebene, Spur (B))
Theorie zur Beschleunigung
Wir haben gesehen, dass ein Wagen, der auf einer schiefen Ebene anfährt, eine Geschwindigkeit hat, die proportional mit der Zeit wächst. Die Funktionsgleichung lautet also:
v(t) = a t
mit der Proportionalitätskonstanten a. Wir nennen a die Beschleunigung (englisch: acceleration).
Es folgt in diesem Fall:
[math]a = \frac{v}{t}[/math]
(Bewegung mit konstanten Beschleunigung aus der Ruhe)
Besitzt der Wagen zu Beginn der Bewegung bereits eine Anfangsgeschwindigkeit v0 , so lautet die Funktionsgleichung
v(t) = v0 + a t
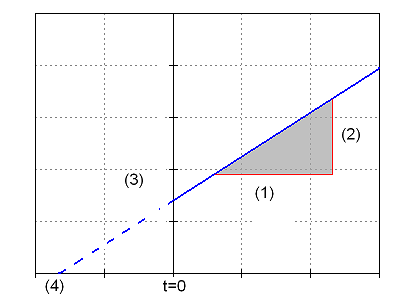
Der Graph ist eine verschobene Ursprungsgerade:
(1)[math]\Delta t[/math]
(2)[math]\Delta v[/math]
(3)v0
(4)t0
Rechtswertachse: Zeit t, Hochwertachse: Geschwindigkeit v
Es ergibt sich für a>0 eine Bewegung mit konstanter Beschleunigung, für a=0 eine Bewegung mit konstanter Geschwindigkeit und für a<0 eine Bewegung mit konstanter Verzögerung (fallende Gerade).
Vorsicht: diesmal ist die Formel [math]a = \frac{v}{t}[/math] falsch!
Es gilt:
[math]a = \frac{\Delta v}{\Delta t}[/math]
a ist also die Steigung der Geraden.
Definition: Die Beschleunigung a ist die Steigung des t-v-Graphen.
Die Einheit der Beschleunigung ist folglich m/s2.
Aufgabe 2.3: Beschleunigungstest
Ein Testinstitut untersucht die Bewegung eines Fahrzeugs. Die Messwerte sind:
| Zeit t in s | Geschwindigkeit v in m/s |
|---|---|
| 0 | 0 |
| 5 | 1 |
| 10 | 2 |
| 60 | 12 |
| 80 | 12 |
| 100 | 12 |
| 110 | 8 |
| 120 | 4 |
| 130 | 0 |
a) Zeichnen Sie ein t-v-Diagramm! (10 s = 1 cm , 1 m/s = 1 cm )
b) Geben Sie die Art der Bewegung in den einzelnen Zeitabschnitten an!
c) Ermitteln sie mithilfe der Zeichnung die Beschleunigungswerte!