Acharya Narendra Dev College/Learning Physics through Problem Solving/Mechanics

Problem 1

How do you determine Rotational Inertia of Geometrical Bodies?

Solution to problem 1

Problem 2

A wheel A of radius [math]r_a[/math] = 10.0 cm is coupled by belt B to wheel C of radius [math]r_c[/math] = 25.0 cm. Wheel A increases its angular speed from rest at a uniform rate of 1.6 rad/[math]s^2[/math]. Find the time that wheel C will take to reach a rotational speed of 100 rev/min, assuming that belt does not slip.

Solution to problem 2

Problem 3

A pulsar is a rapidly rotating neutron star that emits radio pulses with precise synchronisation, one such pulse for each rotation of the star. The period T of rotation is found by measuring the time between pulses. At present, the pulsar in the central region of the Crab nebula has a period of rotation of T=0.033 s, and this period is observed to be increasing at the rate of 1.26 x 10 [math]^-[/math][math]^5[/math] s/y.

(a) What is the value of the angular acceleration in 2 rad/s[math]^2[/math] ?

(b) If its angular acceleration is constant, how many years from now will the pulsar stop rotating?

(c) The pulsar originated in a supernova explosion seen in the year A.D. 1054. What was T for the pulsar when it was born? (Assume constant angular acceleration since then.)

Solution to Problem 3

Problem 4

The oxygen molecule, O[math]_2[/math], has a total mass of 5.30 x 10 [math]^-[/math][math]^2[/math][math]^6[/math] kg and a rotational inertia of 1.94 x 10[math]^-[/math][math]^4[/math][math]^6[/math] kg m[math]^2[/math] about an axis through the centre of the line joining the atoms and perpendicular to that line. Suppose that such a molecule in a gas has a speed of 500 m s[math]^-[/math][math]^1[/math] and that its rotational kinetic energy is two-thirds of its translational kinetic energy. Find its angular velocity.

Solution to problem 4

Problem 5

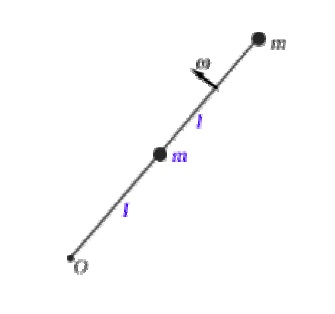
Two particles, each with mass m, are fastened to each other, and to a rotation axis at O, by two thin rods, each with length l and mass M as shown in the figure. The combination rotates around the rotation axis with angular velocity ω. Obtain algebraic expressions for (a) the rotational inertia of the combination about O and (b) the kinetic energy of rotation about O.

Solution to problem 5

Problem 6

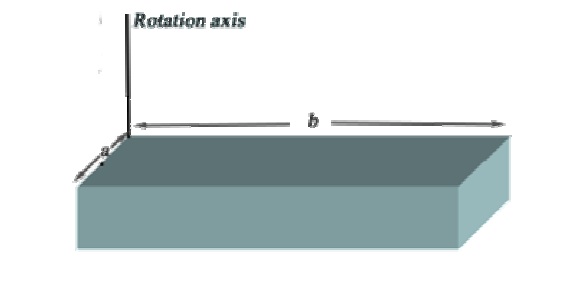
A uniform thin solid block of mass M and edge lengths a and b is as shown in the figure. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces.

Solution to problem 6

Problem 7

(a) Show that the rotational inertia of a solid cylinder of mass M radius R about its central axis is equal to the rotational inertia of a thin loop of mass M and radius R/[math]\sqrt2[/math] about its central axis.

(b) Show that the rotational inertia I of any given body of mass M about any given axis is equal to the rotational inertia of an equivalent loop about that axis, if the loop has the same mass M and radius k given by

k = [math]\sqrt{\frac{ I }{M}}[/math]

The radius k of the equivalent loop is called the radius of gyration of the given body.

Solution to problem 7

Work in progress, expect frequent changes. Help and feedback is welcome. See discussion page.