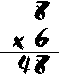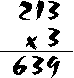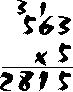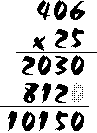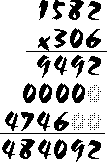ABE Math Tutorials/Whole numbers/Long multiplication

When we multiply 8 x 6, we are actually adding six 8's together (8 + 8 + 8 + 8 + 8 + 8 = 48). Multiplication is just adding, but on a large scale.

It won't come as a surprise, then, to find that multiplying big numbers is very similar to adding big numbers.

Here's a simple example: we are multiplying 213 x 3. First we multiply the digit in the ones' column (the "3" in "213"). This gives us 3 x 3 = 9, and we write "9" in the ones' part of the answer. Then we multiply the digit in the tens' column, and this gives us 3 x 1 = 3, and we write "3" in the tens' part of the answer. Finally, we multiply the hundreds' digit (3 x 2 = 6) and add this to our answer, to give the final: 639.

Here's another example, but with carrying.

In this example, we are multiplying 563 x 5. As you can see, we must first multiply 5 x 3, and the answer to this is "15". But remember -- we can only put one digit in the ones' part of the answer, and "15" has two digits. So we write the "5" in the ones' part and we carry the "1" over to the tens' column. Next, we multiply 5 x 6 = 30 -- but we have to add the "1" that we carried over from the ones' column. This gives us 30 + 1 = 31 for our tens' part of the answer. But once again, we can only write down one digit. We write down the "1" from "31" and we carry the "3" over to the hundreds' column. Now we multiply 5 x 5 = 25; add the "3" from the tens' column to give us 28 for the hundreds' column. We write down the "8" in the hundreds' place, and carry the final "2" over into the thousands' part of the answer. We end up with "2815" as our final answer.

So far, we have been multiplying by only one digit. How about a more complicated multiplication, like 406 x 25?

This example is done mostly like the one above, except that we now have two digits to multiply (both the "2" and the "5" in 25). First, we multiply 406 x 5, just as before. Next, we multiply 406 x 2 -- but we must put the answer to this multiplication one space to the left of the answer above. Some people like to write an extra "0" on the end to hold this space, so that they don't forget. Once you have the two multiplications done, you add them together to get the final answer: 10,150.

Common mistake!When you are doing a long and complicated multiplication, it is easy to add the wrong digits together when you are calculating the final answer. Try to place your digits neatly, one under the other, so that you are adding all the ones' column together, all the tens', etc.

Ready for an even more complicated example? Try to multiply 306 x 1582 -- then see how your work compares with the example shown below:

Note that although the question asked you to multiply 306 x 1582, you can also multiply 1582 x 306 and get the same answer. In multiplication, as in addition, it doesn't matter what order the numbers are in. It is easier to work with the numbers if you put the larger number on the top when you are setting up your multiplication.

Since we are multiplying by a 3-digit number, we will have three multiplications before we add up to get the final answer. Note that the third multiplication (ie. where we multiply 1582 x 3) is moved over two spaces to the left.Did you get 484,092 for your answer?

If so, try these multiplication problems on your own.

1. 714 x 82 =
2. 3054 x 60,416 =
3. 989 x 170 =

If you'd like to check your answers, click here.

If you're ready for the homework, click here.