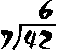ABE Math Tutorials/Whole numbers/Expressing operations

Different Ways of Expressing Operations

Objectives

We will learn division,subtraction,addition and multiplication

Definition

The items listed above are called the basic arithmetic operations

The following is a discussion on Division: As you have seen, there are two different signs to indicate that a division must be done: ÷ This sign means "divided by". For example, 42 ÷ 7 = 6. We read this as: "42 divided by 7 equals 6".

The division bar means "divided into". This question reads "7 divided into 42 equals 6"

There are other ways that we can talk about division problems. We could, for example, ask: "How many times does 7 go into 42?" Or even: "How many 7's are in 42?" The answer, of course, is still "6". The answer to a division problem is called a quotient (pronounced like: "kwoh-shunt"). You might not realize it, but this

is one of the most common ways to show a division. Looks like a fraction, doesn't it? But this also means "42 divided by 7". Sometimes this is written with a "slash" instead, as in "42 / 7".

Discussion on Subtraction: Fortunately, there is only one sign used for subtraction: the " - " sign. When we write "25 - 5", we can say "25 subtract 5" or "25 take away 5" or "25 minus 5" or even "5 less than 25". Whatever we say, it all means the same thing, and the answer (called the difference) is 20. Note that subtraction and division have something in common: it really matters which way you write the operation. For example, "25 - 5" is not the same as "5 - 25" ! Similarly, "42 ÷ 7" is not the same as "7 ÷ 42".

Discussion on Addition: There is only one sign used for addition: the " + " sign. When we write "16 + 7" we read it as "16 plus 7" or "16 and 7" or "16 added to 7". The answer to an addition problem is called a sum: the sum of 16 and 7 is 23. In addition, it doesn't matter which way you write the operation. "16 + 7" will give you exactly the same answer as "7 + 16".

Discussion on Multiplication: You are probably used to seeing the " x " sign used for multiplication. When we write "7 x 8" we can read it as "7 times 8" or "7 multiplied by 8" or even "seven 8's". But there are other ways to express a multiplication. A set of brackets also tells us that a multiplication must be done: 7(8) or (7)8 or even (7)(8) all mean "7 x 8". Another way to show that two numbers are meant to be multiplied together is to put a "dot" between them, as in 7 · 8. (Sometimes you will see this in internet documents with an asterisk instead, as in "7 * 8").The answer to a multiplication problem is called a product. Like addition, multiplication doesn't care which order you write the numbers in. 7 x 8 is exactly the same as 8 x 7, and they both have the same product: 56.

Giving meaning to"Greater than" and "less than": We are all used to seeing the "equals" sign ( = ) when we are working in math. What this sign means, of course, is that the numbers on the left side of the "equals" sign are equal to the numbers on the right side of the sign. For example, we know that:

4 + 2 = 6 or: 7 x 5 = 35 ... and it's obvious that: 12 = 12 Any mathematical statement like this, (with a left side, a right side, and an "equals" sign in between) is called an equation.But what if both sides are not equal? In this case, we do not have an equation, we have an inequality. There are another two signs we can use to talk about an inequality:

the "less than" sign ( < ) the "greater than" sign ( > ) Here are some examples to show how these signs are used: 18 > 11 (we read this as: "18 is greater than 11") 420 < 799 ("420 is less than 799") 4 + 2 > 5 ("4 plus 2 is greater than 5") 7 x 5 < 8 x 9 ("7 times 5 is less than 8 times 9") One way to remember which sign is which, is to memorize that: the "point" or arrow of the sign always points to the smaller number.You can find these signs on your computer keyboard. Often they are right on the "comma" and the "period" keys: you have to hold down the "Shift" key to get them.

Activity

Perform the following operations Which sign would you put between each of these two sides? 15 ___ 21 85 ___ 41 5 + 8 ___ 10 19 - 8 ___ 15

Check your answers?

• 15 < 21
• 85 > 41
• 5 + 8 > 10
• 19 - 8 < 15

For your Expressing Operations homework click here.