Basic Tools in Economic Analysis/Next
LINES AND CURVES
The functional relationship between the variables may be linear or non-linear. A line or a curve is nothing but the locus of various points. A line depicts the relationship between the variables. For example, the relationship between consumption and income as shown in the following diagram:
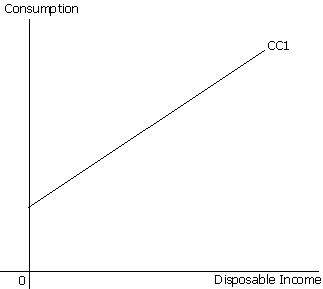
Line CC1 is a straight line and has a positive slope. It depicts that aggregate consumption is positively related to aggregate disposable income. It explains that, an increase in disposable income will promote to an increase in consumption. Many economists try to set up the relationship between economic variables in different ways. One of the most popular and easy method is through curves. A non linear function of graph is depicted in terms of curve. Let us consider the following curves.
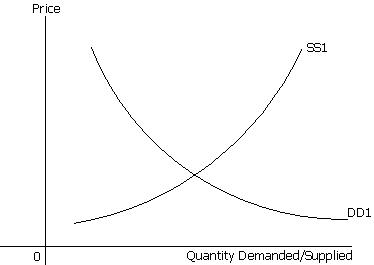
In the following diagram,DD1 is a smooth downward sloping non linear demand curve. It explains the relationship between quantity demanded of good X at various prices. Moreover, SS1 is an upward sloping supply curve. It is also a non-linear curve and shows relarionship between quantity supplied of good X at various prices.
SLOPE
Slope is an important term in modern economic analysis. The slope indicates change in one variable due to a change in other variable. Slope is defined as the amount of change in the variable measured on the vertical or Y axis per unit change in the variable measured on the horizontal or X axis. It is expressed as ∆Y/∆X, where delta (∆) stands for a change in the variable. The slope of a curve is an exact numerical measure of the relationship between the change in the variable Y to change the variable X.
Slope is also popularly termed as ‘the rise over the run’. Here rise is the vertical distance while run is the horizontal distance. The measurement of slope can be shown as follows:
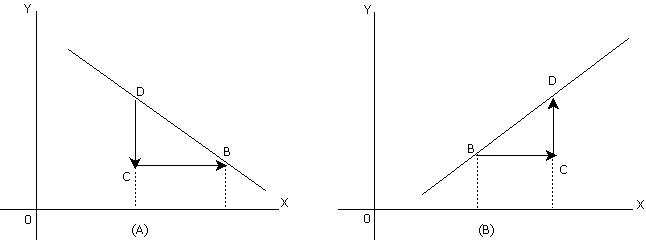
In both the diagrams (A) and (B) slope = vertical distance/horizontal distance. i. e. CD / BC. However, in diagram (A), slope is negative as the relationship between X and Y is inverse. Here units of Y decrease with increase in the units of X. In Diagram (B) the curve is slopping upwards, indicating a positive relationship between X and Y. Here units of Y increase with increase in the units of X.
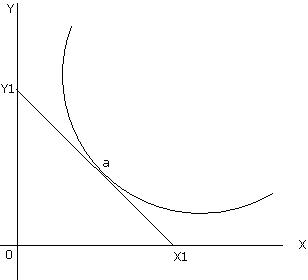
If the curve is non-linear, then its slope changes at various points. Slope on a non-linear curve is measured at a given point by drawing a tangent at the given point and is then measured as the vertical distance/horizontal distance. This is shown in the following diagram with a non-linear curve. We measure slope at point 'a' by drawing a tangent at point 'a'. Y1X1 is the tangent drawn at point 'a'. Slope of the curve at point 'a' is given as 0Y1/0X1
The main properties of slope are:
i) It can be numerically measured.
ii) In case of a straight line, the slope is constant through out the curve.
iii)In case of a non-linear curve, the slope changes through out the curve.
iv) The nature of the relationship between two variables can be indicated with the help of slope. If the slope is negative then it indicates inverse relationship between the two variables and if the slope is positive, it indicates direct relationship.