Basic Tools in Economic Analysis

|

BASIC TOOLS OF ECONOMIC ANALYSIS

Introduction

Economic theories are formulated to explain different phenomenon. They try to explain the relationship between two or more variables. While formulating theories a number of tools are used by experts in this field. The tools of economic analysis are found in the realm of Mathematics. Mathematics is being profusely used in modern economic analysis. Mathematics is regarded as the second language for the students of economics. Geometry is being increasingly resorted to in order to provide pictorial presentation of economic behavior. Diagrams and Graphs provide visual impact and help to grasp and learn economics with interest and ease. A Chinese proverb says “A picture is worth a thousand words”.

Modern economists have turned to Calculus, Matrix, Algebra and Derivatives to use them as fundamental tools to express complicated aspects of economic theories and models more precisely and accurately. All these applications of mathematics are significant as a tools and techniques to impart conciseness, precision and rigour to economic analysis.

In brief, get acquainted with the terms such as Variables, Ceteris Paribus, Functions, Equations, Identities, Graphs and Diagrams, Lines and Curves, Slopes, Limits and Derivatives, Time Series and so on. These are the basic tools of economic analysis.

	Learning Objectives
After reading this chapter, you are expected to learn about:

Concepts

VARIABLES

Variables play an important role in economic theories and models. A variable is a magnitude of interest can be defined and measured. In other words a variable is something whose magnitude can change. It assumes different values at different times or places. Variables that are used in economics are income, expenditure, saving, interest, profit, investment, consumption, imports, exports, cost and so on. It is represented by a symbol.

Variables can be endogenous and exogenous. An endogenous variable is a variable that is explained within a theory. An exogenous variable influences endogenous variables, but the exogenous variable itself is determined by factors outside the theory. 

CETERIS PARIBUS

Ceteris paribus is a Latin phrase meanings, “all other things remaining the same” or all relevant factors being equal. In Economics the term “Ceteris Paribus” is used quite often to assume all other factors to remain the same, while analyzing the relationship between any two variables.

Ceteris Paribus is an assumption which we are compelled to make due to complexities in the reality. It is necessary for the sake of convenience. The limitations of human intelligence and capacity compel us to make this assumption. Besides, without the assumption we cannot reach on economic relations, sequences and conclusions. In fact, there are large number of variables interacting simultaneously at a given time. If our analysis has to be accurate we may have to examine two variables at a time which makes it inevitable to assume other variables to remain unchanged.

For instance, if we try to establish the relationship between demand and price, there may be other variables which may also influence demand besides price. The influence of other factors may invalidate the hypothesis that quantity demanded of a commodity is inversely related to its price. If rise in price takes place along with an increasing in income or a change technology, then the effect of price change may not be the same. However, we try to eliminate the interrupting influences of other variables by assuming them to remain unchanged.

The assumption of Ceteris Paribus thus eliminates the influence of other factors which may get in the way of establishing a scientific statement regarding the behavior of economic variables.

Ceteris Paribus is an assumption which we are compelled to make due to complexities in the reality. It is necessary for the sake of convenience. The limitations of human intelligence and capacity compel us to make this assumption. Besides, without the assumption we cannot reach on economic relations, sequences and conclusions. In fact, there are large number of variables interacting simultaneously at a given time. If our analysis has to be accurate we may have to examine two variables at a time which makes it inevitable to assume other variables to remain unchanged.

FUNCTION

 A 'function' explains the relationship between two or more economic variables. A simple technical term is used to analyze and symbolizes a relationship between variables. It is called a function. It indicates how the value of dependent variable depends on the value of independent or other variables. It also explains how the value of one variable can be found by specifying the value of other variable.

For instance, economist generally links demand for good depends upon its price. It is expressed as D = f (P). Where D = Demand, P = Price and f = Functional relationship.

Functions are classifieds into two type namely explicit function and implicit function. Explicit function is one in which the value of one variable depends on the other in a definite form. For instance, the relationships between demand and price Implicit function is one in which the variables are interdependent.    

EQUATIONS

Economic theory is a verbal expression of the functional relationships between economic variables. When the verbal expressions are transformed into algebraic form we get Equations. The term equation is a statement of equality of two expressions or variables. The two expressions of an equation are called the sides of the equation. Equations are used to calculate the value of an unknown variable. An equation specifies the relationship between the dependent and independent variables. Each equation is a concise statement of a particular relation.

For example, the functional relationship between consumption (C) and income (Y) can take different forms.The most simple equation; C = a (Y) states that consumption (C) is related to income (Y). It says nothing about the form that this relation takes.

Here ‘a’ is constant and it has a value greater than zero but less than one (0<a<1). Thus the equation shows that C is a constant proportion of income. For instance, if ‘a’ is 1/2then the consumer would always spend 50% of the income on consumption. The equation shows that if income is zero, consumption will also be zero.  

C = a + b Y is yet another form of consumption function. Here value of a is positive and b is 0<b<1.

IDENTITIES

An identity explains an equilibrium condition or a definitional condition. A definitional identity explains that two alternative expressions have exactly the same meaning. For example, total profit is defined as the excess of total revenue over total cost, and we can denote as:

π ≡  TR - TC

Where π is total profit, TR is total revenue and TC is total cost.

Similarly, saving is defined as the difference between income and consumption expenditure and we can say;

S ≡  Y - C

You are required to note that an identity is denoted by a three - bar sign (≡).

The distinction between an identity and an equation is very subtle and important. An identity is a relation that is true for all values of the variables; no values can be found that will contradict it. For instance, (x + y)² = x² + 2xy + y² is an expression which is true for any numerical value of x and y. Identities are statements that are compatible with any state of the universe. In case of National Income accounting we have an important identity between National Income (Y) ≡ National Output (O) ≡ National Expenditur (E) 

Hence; Y ≡ O ≡ E

Identities are mere “truisms”, they cannot form the basis of any theory.    

GRAPHS AND DIAGRAMS

A graph or a diagram presents the relationship between two or more sets of data or variables that are related to one another. Graph is most commonly used tool in modern economics. Graph depicts the functional relationship between two or more economic variables. The use of graph provides a better understanding of the economic generalizations. Graph presents a visual picture of an abstract idea. Also it is useful for accuracy and precision.

Graph can be drawn only two dimensional figures on a plain paper. It represents the values of only two variables at a time. The common method of constructing a graph or a diagram is described below:

A graph has a horizontal line termed as X axis and a vertical line termed as Y axis. The point of intersection between X and Y axis is termed as 'origin' point.

The surface is divided into four parts, each part is called a quadrant. The four quadrants are numbered in anticlockwise direction as depicts in following diagram.

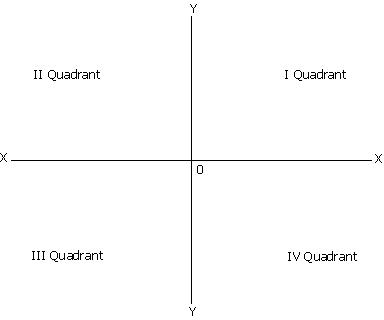
The first quadrant depicts the positive values of both X and Y. It is called positive quadrant. Generally, economic theories are deals with the positive quadrants.

At times the terms “Graph” and “Diagram” are used interchangeably. Diagrams, like graphs, are pictorial presentations. Diagrams may be in the form of figures such as explaining the circular flow of national income. Graphs are quite meticulous whereas diagrams can be based on abstraction. For instance, Pie diagram is a best example of a diagram that indicates through slicing the percentage- wise composition of a phenomenon, such as how much percentage of national income is generated from which sector of the economy.

Next