Secondary Mechanics/Page2: Linear Motions

back to the previous page

In order to measure a movement, we need one

• coordinate of location x and one
• coordinate of time t.

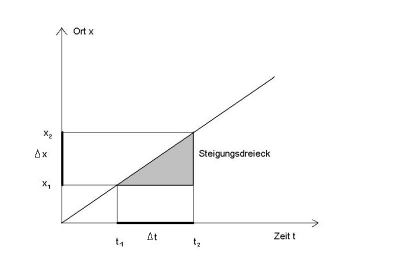
The local difference is then delta x:
[math]\Delta x[/math] = x₂ - x₁

(Local coordinate at the end minus local coordinate at the beginning of the time interval)

Correspondingly the time interval [math]\Delta t[/math]:
[math]\Delta t[/math] = t₂ - t₁

Thus the speed becomes

Definition

v = [math]\frac{\Delta x}{\Delta t}[/math]

(distance through time)

Note: This is a quotient out of differences,

If we take two neighbouring measuring points, then we get the momentary speed of the cart tum to time t₁ and/or, we take first and the 51 to t₂. , We get the average speed in the time interval to measuring point

[math]\Delta t[/math] = t₅₁ - t₁

The movement can be represented graphically in a time-location diagram (t-x-diagram):

constant speed

Assignment

Task of 1.2: Draw a time location diagram each for cart A and B! Select the units suitably! Lösung

Task 1.3: snail mail

Two snails move uniformly and upright in a garden:
The first snail moves with 1 mm / s, the second in 2 s by 4 mm.
After 2 s and remains the second but suddenly snail.
If the first snail second outdated, they doubled their speed, while the second half with early speed creeps.
a) Draw a common x-t-diagram!
(1s = 1 cm ; 1 mm = 1 cm)
b)Represent the dependence of the speeds of the time for both movements in a diagram!
(1 s = 1 cm; 0,5 mm/s = 1 cm.)

Tip

Solution

Task 1.4: driving styles

A distance of 300 km is in a car back. Calculate the time needed to when

• a) the speed of 75 km / h,
• b) one half of the road at 50 km / h, the other with 100 km / h retired,
• c) half the journey time of 50 km / h, the other with 100 km / h driven. (Solution for example by guessing and subsequent graphical or computational review!)
• d) a third of the running time with 66 km / h, two-thirds of 87 km / h back! (Note: Creative Problem Solving needed: either algebraically about solving equations with 2 2 unknowns, or graphically with accounting review of the solution! )
  

Draw on each sub-task also a time-location-diagram! (100 km = 5 cm, 1 h = 4 cm) Solution

next page