Mechanics11/Page3
interpretation of time local diagrams
Assignment
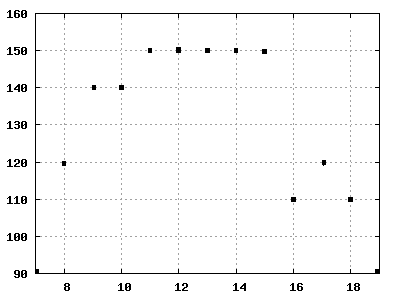
Desiree and Marc go by bike to the plan lake. They drive off at 8.00 o'clock and arrive around 19.00 again at home.
Along the road are kilometer stones. They note each full hour their position x.
- a) calculation it for each time interval of 1 hour the average speed! Use calculation formulas!
- b) describing it for each time interval the process of the movement in words! Possible interpretation?
- c) calculation it the average speed for the first 4 hours! How can this be plotted?
1. Motion equation
We deduce a general equation for straight-line-homogeneous movements: from
[math]v = \frac{\Delta x}{\Delta t} = \frac{x - x zero}{\Delta t}[/math]
follows
x = x0 + v[math] \Delta t[/math]
Thus the current position at the end of one time interval can be computed e.g. with well-known initial place x and well-known speed of v.
At present if we take for x0 the place x (0) to t = 0, then those results
1. Motion equation:
x (t) = x0 + v t
sample calculation
Assignment
Problem 1.6: Flight competition Bussard flies with a falcon around the bet. The bussard gets 14 km projection/lead from the starting point measured, because it is clearly slower with 95 km/h than the falcon (153 km/h).
- a) when and where the falcon catches up the bussard?
- b) who wins the flight up to the summit cross of the Hörnle (40 km from the start )?