Mechanics11/Seite8

zurück zur letzten Seite

Trägheitskräfte in verschiedenen Bezugssystemen

Gedankenexperiment: Wagen Huckepack

Ein (kleines) Versuchswägelchen befindet sich auf einem (großen) Versuchswagen. Ein Beobachter A steht neben dem Versuch in einem ruhenden Bezugssystem. Beobachter B sitzt auf dem großen Versuchswagen. Nun wird der große Wagen aus der Ruhe beschleunigt.

Wir können uns zum Beispiel vorstellen, wir stehen als Beobachter B in einer beschleunigenden U-Bahn, während A auf dem Bahnsteig zurück bleibt, und der kleine Wagen ist ein Skateboard im Mittelgang der U-Bahn.

Was passiert?

Richtig: Der kleine Wagen macht die Beschleunigung nicht mit. Er bleibt für Beobachter A in Ruhe bis der große Wagen unter ihm weg gefahren ist, dann fällt er herunter. Auf ihn wirkt schließlich keine beschleunigende Kraft.

Beobachter B dagegen registriert eine Beschleunigung des kleinen Wagens nach hinten, und schließt daraus auf eine beschleunigende Kraft F . Wenn er möchte, kann er sie mit einem Kraftmesser messen. Es handelt sich um die so genannte Trägheitskraft des Wägelchens, denn sie hat ihre Ursache in der Trägheit des kleinen Wagens.

Im ruhenden System von A tritt die Kraft F nicht auf.

Wir stellen fest:

Trägheitskräfte treten nur in beschleunigten Bezugssystemen auf.

Aufgabe 3.1

Ein Fahrgast in einem Karussell erfährt je nach dem, in welchem Bezugssystem seine Bewegung betrachtet wird, verschiedene Kräfte.

• a)Bezugssystem eines ruhenden Beobachters außerhalb des Karussells
• b)Bezugssystem des Fahrgastes im Karussell

Zeichnen Sie jeweils die auf den Fahrgast wirkenden Kräfte ein und ordnen Sie ihnen die Bezeichnungen Fliehkraft (= Zentrifugalkraft) und Zentralkraft (= Zentripetalkraft) zu. Welche Kraft ist eine Trägheitskraft?

Lösung

Nun wollen wir die beschleunigenden Kräfte bzw. die Trägheitskräfte quantifizieren.

Vorüberlegungen:
Offensichtlich besteht ein Zusammenhang zwischen der Masse des beschleunigten Körpers, seiner Beschleunigung und der dabei wirkenden Kraft. Zum Beispiel brauchen wir mehr Kraft, einen schweren Körper zu beschleunigen wie einen leichten.

Beispiel: Es ist viel leichter ein Fahrrad anzuschieben wie ein Auto.

Im Klartext: Je größer die Masse m eines Körpers ist, desto mehr Kraft F ist erforderlich, um eine bestimmte Beschleunigung a zu erreichen.

Vorsicht: Dies ist lediglich eine Je-Desto-Aussage, also eine Monotoniebeziehung zwischen den Größen A und B: Steigt A (die Masse), so auch B (die Kraft), wenn C (die Beschleunigung) dabei konstant bleibt.

Es gilt also:
m größer ⇒ F größer bei a = konstant
Aber auch:
F größer ⇒ m größer bei a = konstant

Also zusammen

Für a = konstant  gilt:  m größer  ⇔  F größer

Aufgabe 3.2: Formuliere entsprechende Monotoniebeziehungen

für den Fall

• a) m = konstant
• b) F = konstant

Lösung

2. Newtonsches Gesetz (NG2)

Nun wollen wir den Zusammenhang zwischen der Kraft, der Masse und der Beschleunigung quantitativ untersuchen. Alle drei Größen lassen sich direkt oder indirekt messen, was uns die Möglichkeit gibt, systematische Versuche anzustellen. Wir befragen die Natur!

Betrachten wir zunächst den Versuchsaufbau:
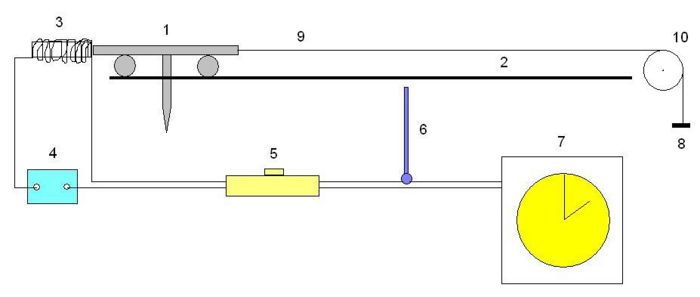
Das Kernstück der Anordnung ist eine Rollenfahrbahn mit einem Versuchswagen bekannter Masse m . Er wird durch die Kraft eines Gewichts beschleunigt, das mittels einer Schnur, die über eine Umlenkrolle läuft, an ihm zieht. Die Beschleunigung des Wagens wird aus der Fahrzeit berechnet, die der Wagen benötigt, um eine Strecke von 1,00 m zurückzulegen. Diese Zeitdauer messen wir mit einer elektrischen Uhr, die beim Start ausgelöst und nach 1,00 m automatisch gestoppt wird.

1. Versuchswagen
2. Rollenfahrbahn
3. Elektromagnet
4. Stromquelle
5. Tastschalter
6. Klappschalter
7. elektrische Stoppuhr
8. Gewicht
9. Schnur
10. Umlenkrolle

Details zum Versuchaufbau: die Fahrbahn wird wieder leicht geneigt, um die Reibung auszugleichen. Der Wagen wird zunächst mit einem Elektromagneten in der Ausgangsposition festgehalten. Mit einem Tastschalter wird nun gleichzeitig der Stromkreis für den Elektromagneten ausgeschaltet und der Stromkreis für die elektrische Uhr geschlossen. Der Wagen fährt los, die Uhr läuft. Durchfährt der Wagen den Klappschalter am Ende der Strecke, so wird die Zeitmessung automatisch gestoppt. Das Gewicht lässt sich für verschiedene Zugkräfte in Schritten von jeweils 10 g erhöhen.

Versuchsreihe 1

m = konstant, gesucht ist der Zusammenhang zwischen der Kraft F und der Beschleunigung a.

Schülerbeitrag: Versuchsergebnis

Masse des Gewichts in g	t in s (Gruppe 1)	t in s (Gruppe 2)	a in m/s2 (Gruppe 1)	a in m/s2 (Gruppe 2)
10	3.49	3.4	0.164	0.173
20	2.70	2.33	0.274	0.368
30	1.96	2.15	0.520	0.432
40	1.69	1.86	0.700	0.578
50	1.54	1.53	0.843	0.854

Aufgabe 3.3: Versuchsauswertung

Tragen Sie die Messwerte der beiden Gruppen in ein geeignetes Diagramm ein, zeichnen sie eine Ausgleichsgerade, die die Messwerte möglichst gut trifft und bestätigen Sie damit den Zusammenhang

Die Beschleunigung a wächst proportional zur Zugkraft F an.

Versuchsreihe 2

Voraussetzung: F = konstant

Jetzt lassen wir die Masse des Zuggewichts gleich und verändern die Masse des Wagens, indem wir daran einige Massenstücke zusätzlich befestigen. Wieder messen wir die Fahrzeiten für eine Strecke von 1,00 m aus der Ruhe und berechnen daraus die Beschleunigungen.
Ergebnis:

Die Beschleunigung verhält sich umgekehrt proportional zur Masse.

Das heißt z. B.: doppelte Masse, halbe Beschleunigung.

Versuchsreihe 3

Voraussetzung: a = konstant

Wir ermitteln das Ergebnis im Gedankenversuch und bestätigen es im Experiment. Verdoppeln wir z. B. die Masse, so ist die doppelte Zugkraft erforderlich, um die gleiche Beschleunigung zu erzielen. (In Gedanken wird jede Hälfte der doppelten Masse getrennt beschleunigt.)
Ergebnis:

Die zur Beschleunigung nötige Zugkraft ist proportional zur Masse. 

Es gilt also

1. F ~ a bei m = konstant
2. 1/a ~ m bei F = konstant
3. F ~ m bei a = konstant

Fassen wir die drei Beziehungen in eine, so gilt

F ~ m*a

Die Formel ist von so großer Bedeutung, dass nach ihr das SI-Einheitensystem justiert wurde. Deshalb ist der Proportionalitätsfaktor 1 (!) Folglich gilt

2. Newtonsches Gesetz (NG2)

F = m*a

In Worten: Kraft ist Masse mal Beschleunigung

Es ergibt sich die Einheitengleichung

1 N = 1 kg*m/s2

Berechnungsbeispiel:
Ein Zug, bestehend aus einer Lokomotive und 8 gleiche Waggons, beschleunigt aus dem Stand mit a = 0,50 m/s². Dazu muss die Lok der Masse 84 t eine Zugkraft von 122 kN aufbringen. Welche Masse hat ein Waggon?

Lösung:
[math]F = m*a[/math]
[math]m = \frac {F}{a}[/math]
m = 244 t
m_Waggon = 20 t

weiter zur nächsten Seite