Mechanics11/Seite4/Loesung1.8
Schülerlösung
b) In diesem Fall handelt es sich nicht um eine gleichförmige Bewegung, da die Geschwindigkeit des Fahrzeugs nicht konstant bleibt, sondern sich immer erhöht
V = s/t
V = 12m : 4s = 3m/s falsch
V = 68,1m : 7,5s = 9,08m/s
V = 93,6m : 9s = 10,4m/s
V= 156,5m : 12,7s = 12,32m/s
V= 178,6m : 14s = 12,76m/s
VDurchschnittsgeschwindigkeit = (3m/s + 9,08m/s + 10,4m/s + 12,32m/s + 12,76m/s) : 5 = 9,512m/s falsch
Lösung von user:Christina
Kommentar: Vorsicht: Zur Zeit t = 0 kennen wir den Ort des Fahrzeugs nicht.
VDurchschnittsgeschwindigkeit graphisch ermitteln, da die Zeitabschnitte nicht gleich groß sind!
Schülerlösung 2
b) Es kann sich um eine gleichförmige Bewegung handeln muss es aber nicht.
Geschwindigkeitsberechnung:
v =[math]\frac{\Delta x} {\Delta t}[/math] = [math]\frac{x_1 - x_0} {t_1 - t_0}[/math]
v =[math]\frac {93,6m - 68,1m} {9,0s - 7,5s}[/math] = 17[math]\frac{m}{s}[/math]
In km/h:
17[math]\frac{m}{s}[/math] * 3,6 =[math]61,2 \frac{km} {h}[/math]
--Kenny 12:23, 19 October 2007 (CEST)
--Marc 12:24, 19 October 2007 (CEST)
Teacher's Solution
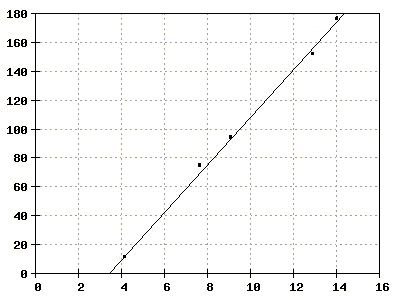
Die Messwerte liegen nicht genau auf einer Geraden, da natürlich Messfehler enthalten sind. Die sog. Ausgleichsgerade trifft die Messpunkte möglichst genau.
An ihr lässt sich nun ein Steigungsdreieck anlegen. Wir lesen z.B. ab:
[math]\Delta[/math]t = 14,2 s - 3,5 s = 10,7 s
[math]\Delta[/math]x = 180 m - 0 = 180 m