Ángulos
| GEOMETRÍA EUCLIDIANA |
Ángulos | Paralelas cortadas por una secante | Áreas y Perímetros | Volumen de Cuerpos Geométricos | Teorema de Pitágoras | Trigonometría |
En este módulo aprenderás los nombres de los diversos tipos de ángulos. También conocerás los dos sistemas de medición de los ángulos y la relación entre las unidades de medición
Contents
- 1 Objetivos
- 2 Objetivos
- 2.1 Conceptos clave del módulo
- 2.1.1 Definición de Ángulo
- 2.1.2 Tipos de Ángulos según su medida
- 2.1.3 Tipos de Ángulos según su posición relativa
- 2.1.4 Ángulos formados por dos rectas paralelas y una secante.
- 2.1.5 Tipos de Ángulos según la suma de sus medidas
- 2.1.6 Tipos de Ángulos según su orientación
- 2.1.7 Conversión de medidas de ángulos
- 2.1.8 Equivalencias entre grados sexagesimales y radianes
- 2.1.9 Esquema-resumen
- 2.2 Ejercicios Resueltos
- 2.3 Recursos en línea
- 2.1 Conceptos clave del módulo
- 3 Web Resources
- 4 ÁNGULOS
- 5 ÁNGULOS
- 6 ¿VERDADERO O FALSO?
Objetivos
Al terminar de estudiar este módulo serás capaz de:
|
Conceptos clave del módulo
Definición de Ángulo
Ángulo es la abertura entre dos líneas rectas que se encuentran en el mismo plano y se intersectan (rectas secantes), el punto de intersección de éstas recibe el nombre de vértice. Los sistemas de medición más comunes para obtener la magnitud de un ángulo son: el sistema sexagesimal (grados), y el sistema cíclico (radianes).
Tipos de Ángulos según su medida
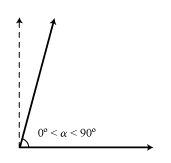
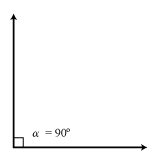
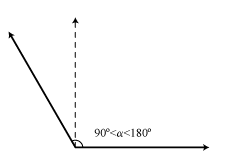
| Ángulo Agudo | Ángulo Recto | Ángulo Obtuso |
|---|---|---|
| Es aquél cuya magnitud es menor que 90º | Es aquél cuya magnitud es igual a 90º | Es aquél cuya magnitud es mayor que 90º |
|
|
|
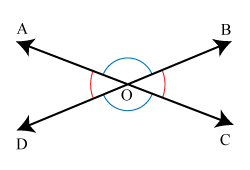
Tipos de Ángulos según su posición relativa
Propiedades de los ángulos Adyacentes.
Se cumple que:
[math]\angle COB + \angle BOA = 180^\circ\,\![/math]
Propiedades de los ángulos Opuestos por el Vértice.
Se cumple que:
[math]\angle COB = \angle AOD[/math]
[math]\angle BOA = \angle DOC[/math]
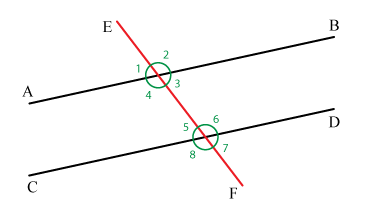
Ángulos formados por dos rectas paralelas y una secante.
Cuando una línea recta transversal o secante intersecta dos rectas paralelas, se forma un conjunto de ocho ángulos cuya posición relativa ha sido profusamente estudiada. Matemáticamente se expresa así:
Dadas las rectas [math]\overline{AB} \parallel \overline{CB}[/math] y [math]\overline{EF}[/math] , se forman los siguientes ángulos:
Considerados de dos en dos, estos ángulos reciben los nombres siguientes:
| Nombre | Descripción | Propiedades |
|---|---|---|
| Alternos Internos | Son dos ángulos internos no adyacentes, situados en distinto lado de la secante | [math]\angle 3 = \angle 5[/math] [math]\angle 4 = \angle 6[/math] |
| Alternos Externos | Son dos ángulos externos no adyacentes, situados en distinto lado de la secante | [math]\angle 1 = \angle 7[/math] [math]\angle 2 = \angle 8[/math] |
| Opuestos por el vértice | Son aquéllos que tienen el vértice en común y los lados de uno de sus ángulos. | [math]\angle 1 = \angle 3[/math] [math]\angle 2 = \angle 4[/math] |
| Correspondientes | Son dos ángulos no adyacentes, situados en un mismo lado de la secante, uno interno y otro externo | [math]\angle 1 = \angle 5[/math] [math]\angle 2 = \angle 6[/math] |
| Colaterales Internos (Suplementarios) | Son dos ángulos internos no adyacentes, situados en un mismo lado de la secante | [math]\angle 4 + \angle 5=180^\circ[/math] [math]\angle 3 + \angle 6=180^\circ[/math] |
| Colaterales Externos (Suplementarios) | Son dos ángulos externos no adyacentes, situados en un mismo lado de la secante | [math]\angle 1 + \angle 8=180^\circ[/math] [math]\angle 2 + \angle 7=180^\circ[/math] |
| Adyacentes (Suplementarios) | Son aquéllos que tienen un lado en común. | [math]\angle 1 + \angle 2=180^\circ \qquad \angle 5 + \angle 6=180^\circ[/math] [math]\angle 2 + \angle 3=180^\circ \qquad \angle 6 + \angle 7=180^\circ[/math] |
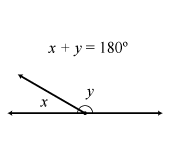
Tipos de Ángulos según la suma de sus medidas
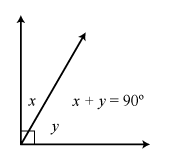
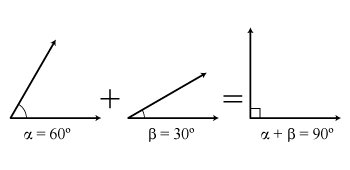
| Ángulos Complementarios | Ángulos Suplementarios |
|---|---|
| Son aquellos cuya suma es igual a 90º | Son aquellos cuya suma es igual a 180º |
|
 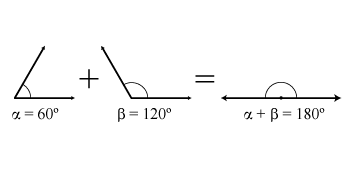
|
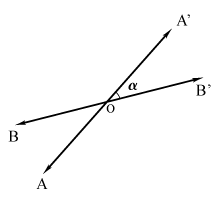
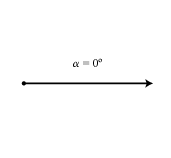
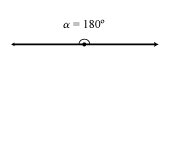
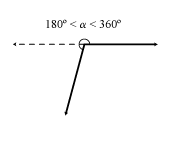
Tipos de Ángulos según su orientación
Los ángulos pueden considerarse "sin orientación", sin embargo cuando sea necesario considerar el sentido de un giro se dotará de signo al ángulo correspondiente.
| Ángulos Positivos | Ángulos Negativos |
|---|---|
| Son aquéllos que abren en sentido opuesto a las manecillas del reloj. | Son aquéllos que abren conforme el sentido de las manecillas del reloj. |
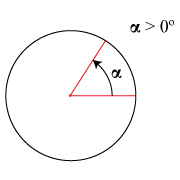
|

|
Conversión de medidas de ángulos
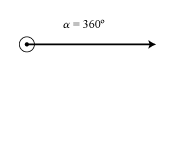
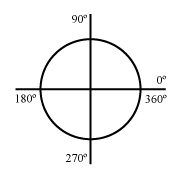
Un grado sexagesimal es la medida del ángulo central de un círculo, de amplitud igual a la 360 ava parte del mismo.
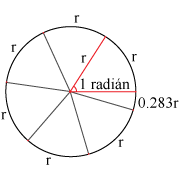
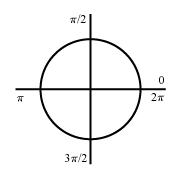
Un radián se define como la medida de un ángulo central cuyos lados cortan un arco de igual longitud al radio del círculo. Ya que la longitud de este arco es igual a un radio del círculo, se dice que la medida de este ángulo es un radián y equivale a 57.296º.
El uso de radianes en vez de grados ayuda a simplificar muchas fórmulas trigonométricas.
1) Para convertir de grados a radianes, se multiplica por [math]\pi\,\![/math] y se divide entre 180º; y se simplifica. Es decir:
| [math]\text {rad =}\text{ grados }\cdot\frac{\pi}{180^\circ}[/math] |
2) Para convertir de radianes a grados, se multiplica por 180º y se divide entre [math]\pi\,\![/math]; y se simplifica. Es decir:
| [math]\text {grados =}\text{ rad }\cdot\frac{180^\circ}{\pi}[/math] |
Equivalencias entre grados sexagesimales y radianes
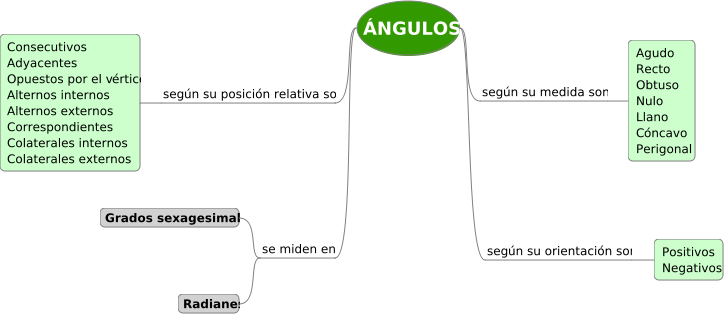
Esquema-resumen
Ejercicios Resueltos
Ir a: Ejercicios Resueltos - Angulos
Recursos en línea
Autoevaluación
WikiQuiz 1
WikiQuiz 2
WikiQuiz 3