Lesson 3: Zero and Negative Indices

Introduction

You have already learnt from the beginning of the topic that an index form is an easy way of writing down numbers.Let us take a look at the example 3⁴.The number 4 is called the index and the number 3 is the base. so 4⁰ also indicates that 0 is the index and 4 is the base. The index which is also called the power or exponent can be positive, negative or zero.

Objectives

By the end of this lesson you should be able to give the value of any number raised to the power 0, solve exercises where the zero index is used, solve problems with negative indexes.

Lesson Content

Let us now consider the zero index. Here is an example.b⁵/b⁵.This as you have already learnt is solved by maintaining the base and subtracting the second index from the first.In this case is b^5-5=b⁰.Also it can be solved as b⁵/b⁵=1.Because of these two scenario it is logical to conclude that any number or letter raised to power zero equals one.Now try to find answers to the following:

1. 7⁰
2. 90⁰
3. a⁰

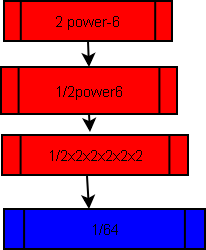
If you remember well then all the answers will be 1.If you got the right answers then BRAVO you have made a great progress. Let us now take a look at the negative indices.a³/a⁷.This is the same as a^3-7 which is equal to a^-4.a^-4=1/a⁴.We can now agree also that any number or letter raised to a negative index can be written as 1 divided by the positive power in question.For instance r^-5= 1/r⁵simplying further 1/r⁵=1/rxrxrxrxr.Let us now use numbers. 2^-6=1/2⁶ 1/2⁶=1/2x2x2x2x2x2

              =1/64

Illustration.

Try these without looking at the solutions. (1/2)^-3, y^-4

Let us find out together. 1/2^-3=1/(1/2)³

               =1/1/8                      
               =1x8/1
               =8

y^-4 = 1/y⁴

               =1/yxyxyxy

How did it go? Hope you got the answers.

Summary

{{{1}}}

Assignment

Now do the following 4<-3</sup> 5-4x90 (9/16)-1/2

Reading

Oweibo K and D Evbuomwan,Jamb and O'Level,Notes and worked Examples.p.1-4. Aina et al Access Mathematics.p.16-18