Depreciating Capital Costs

The value of a capital asset may change over its working life. If its value goes up, we refer to this as appreciation. For example, if the sale price of a work of art continues to increase faster than the rate of inflation, we would say that it is appreciating in value. In most cases, however, the value of the asset decreases as it is used up, and we call this phenomenon depreciation. While accountants have devised very sophisticated ways of calculating how the value of an asset depreciates or decreases over time, this unit outlines three main approaches, each of which is discussed separately below.

Simple Depreciation

The easiest method to understand is Simple Depreciation, which is based on the assumption that the value of the capital asset decreases by an equal amount each year of its working life. In order to calculate the amount of annual depreciation, the price originally paid for the item (its capital cost) is divided by the number of years during which it will be used. This calculation is expressed in the following equation:

Equation for Simple Depreciation:

AD = CC ÷ N

Where:

AD = Amount of Annual Depreciation

CC = Capital Cost

N = Number of years in working life

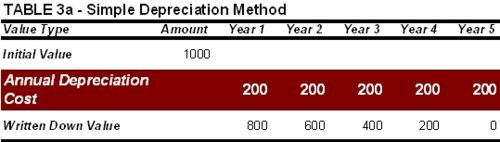
For example, if you buy a laptop computer for €1,000 and expect to use it for a period of five years before buying a replacement, the equation for Simple Depreciation indicates that you will use up €200 of its value each year. These calculations are illustrated in Table 3a below.

Annual Loss of Value using Simple Depreciation Method

The written down value is a notional figure that represents the un-depreciated part of the asset, which continues to decline over its working life. So, if the original price of the laptop was €1,000 and a fifth of its value (€200) is ‘used up’ each year, then its written down value after you have used it for one year is €800. The Simple Depreciation approach assumes that the asset has almost no residual value at the end of the period, when its written down value should be equal to zero. Such an assumption would not be unusual for computer equipment, which becomes outdated very quickly.

Activity

Exercise 3.2 Open the Hülsmann resources in a new window. Go to Section 3 – Elements of cost analysis. At the bottom of the starting page, select Part 1 – Capital & operating costs. Scroll down to Activity A4 – Depreciating capital costs and open the Excel workbook. Follow the instructions.

Social Discount Approach

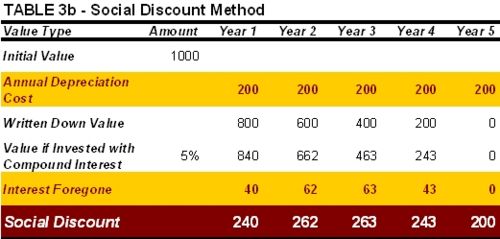
If you had deposited your € 1,000 in a bank five years ago instead of buying a laptop, it would have earned interest during the intervening period and you would now have more money to spend. This example illustrates the fact that there is a cost that arises from having your capital tied up in an asset, regardless of whether you use it or not. The value lost each year should thus include not only the annual depreciation cost but also the interest you could have earned but decided to forego. The Simple Depreciation method does not account for foregone interest.

The Social Discount method of calculating depreciation was devised in order to reflect the actual costs of expending public funds to acquire a capital asset as opposed to investing them for future use. The Social Discount approach accounts for the “value judgement concerning the cost to society” of consuming resources in the present in the expectation that their value will increase when compared to setting them aside for future use (Rumble 1997, page 44).

Determining the Social Discount involves calculating the annual loss of value through simple depreciation and adding the interest foregone on the un-depreciated value of the asset. If instead of spending your money to buy a laptop computer you had been able to lease one at €200 per year (paid in advance), you would still have had € 800 to deposit in the bank earning interest at 5% per annum. At the end of the first year, the amount in the bank would have increased by €40. Thus, the real cost of owning the laptop would be the annual depreciation cost of €200 plus the loss of the opportunity to earn interest of €40. For subsequent years, the amount of interest foregone fluctuates because the un-depreciated value of the laptop continues to decline and the calculation of interest foregone has been compounded from the start of the period.

Annual Loss of Value using Social Discount Method

Table 3b illustrates the calculation of the amounts that should be accounted for each year if we apply the Social Discount method to the purchase of a laptop:

Annualization

A significant problem with the Social Discount method is that it yields different values for each year of the asset’s working life. Common sense suggests that its value is used up at about the same rate from year to year, and this means that the Social Discount rate does not seem plausible, except in certain circumstances.

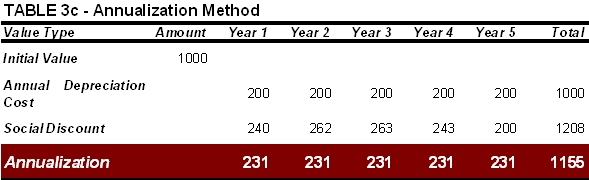
With the Annualization method, the total amount of interest foregone is averaged over the life of the asset, so that the resulting figure is the same from year to year. In general, this is more convenient when reckoning multi-annual depreciation.

Annual Loss of Value using Annualization Method

In Table 3c we continue with the example of the laptop. Using the Annualization approach, the ‘real’ cost of buying a laptop (as opposed to leasing one) would be €231 each year. Compare this with the values in Table 3b above, which vary between €200 and €263 when the Social Discount method is used.

The simplest way to determine the figure to be used for Annualized depreciation involves multiplying the original purchase price (€1,000 in the example above) by an annualization factor (0.231 in this case). This factor can be found in an annualization table which provides different values depending upon the prevailing rate of interest and the expected life of the capital asset.

Activity A.7 in the Hülsmann resource provides an interactive table for calculating annualization factors. If necessary, however, the annualization factor can be calculated using the following formula:

Equation for Annualization Factor:

a(r,n) = [r(1 + r)ⁿ] / [(1+r)ⁿ - 1]

Where:

a(r,n) = Annualization Factor

r = prevailing rate of interest

n = usable life of capital asset.

The equation looks quite complex, but it is simply a reworking of the formula for compound interest and can be carried out on most calculators.

Activity

Exercise 3.3 Open the Hülsmann resource in a separate window. Go to Section 3 – Elements of cost analysis. At the bottom of the starting page, select Part 1 – Capital & operating costs. Scroll down to Activity A6 – Comparing depreciation and annualization and open the Excel workbook. Follow the instructions.

When to Use Different Methods for Depreciating Capital Costs

When is it appropriate to use the different methods discussed above?

In general, the Social Discount approach is not recommended because it produces a different amount of depreciation from year to year, which complicates the process of estimating costs or producing accounts.

The Annualization approach is based on the assumption that the money available can be spent on something else or invested for future use. However, in many cases, ODL institutions do not have complete freedom with regard to the use of funds. In some cases, money is ‘ring-fenced’, which means that it has been given on the condition that it be used only for a specified purpose. Alternatively, donors may demand that funding be returned if it is not used within a specified period. In such cases, the Simple Depreciation method should be used.

However, when funds are not ring-fenced and there is a genuine alternative for their use, then the Annualization approach may be a more appropriate way of calculating depreciation of capital assets. This is particularly true when preparing cost estimates for using different forms of technology to deliver an ODL course or programme. In addition, if the capital asset will need to be replaced at some point in the future (for example, computer equipment), then the Annualization approach will come closer to reflecting the actual replacement cost than the simple depreciation method.

Self Assessment

Simple Depreciation or Annualization This exercise can be carried out on your own, with a partner or as a team. Click on the link for Exercise 3.4 and follow the instructions. Feedback: When you have completed the exercise, you can check you answers by going to Exercise 3.4 - Answer Sheet

Reading

Other Resources Rumble, G. 1997. The Costs and Economics of Open and Distance Learning. Chapter 6, pages 42-50. Hülsmann, T. 2004. Costing Open and Distance Learning. Section 3.1: ‘Elements of Cost Analysis, Capital and operating costs’, pages 9-13.