User:KirbyUrner/Collaborations
This is not a complete list of every project I've worked on, just a sample of some of the more salient ones.
Contents
[hide]Educational
Synergetics on the Web
Since I started reading Bucky Fuller works with gusto, starting in the early 1980s, I've endeavored to be one of his chief commentators, starting with my web site, Synergetics on the Web, and following up with a published essay called Synergetics: The Invention Behind the Inventions. I worked with both Kiyoshi Kuromiya and Ed Applewhite on some of these Fuller-related projects. Kuromiya and I snagged the BFI.org domain name and I served as BFI's first webmaster, in addition to developing my own sites.
Synergetics is a philosophical language Fuller invented and attempted to share with others. It might be categorized as a flavor of Neo-Platonism in that it strongly distinguishes between Forms in pure principle, specified in terms of angles alone, and ordinary spatio-temporal objects, specified in terms of angle and frequency. His "frequency" concept relates to standard scientific uses around energy and the electromagnetic spectrum.
Fuller consistently distinguished between "mind" and "brain" in his philosophy, associating the former with intuition, the latter with storage and recall. He considered thinking as a kind of "connecting the dots" activity, wherein the dots were special case realizations (experiences) that might nevertheless communicate more timeless principles thanks to their organization into "systems" which he modeled as sphere-like and described as "connecting around in all circumferential directions" (the omni-directional halo concept).
In today's nomenclature, we might use this analogy: the brain stores web pages (apprehends) while the mind adds the hyperlinks (comprehends).
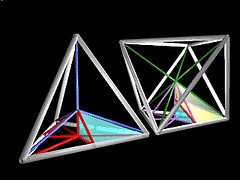
One innovation that characterizes these "explorations in the geometry of thinking" is Fuller's insistence on the tetrahedron as the primordially most primitive shape. Given his bias towards the discrete and the digital (the quantum), perfect continua were banished from his thinking, so that spheres come across as relatively complex, having more constituent topological features than the simple simplex (the tetrahedron).
This emphasis on tetrahedra led him to (a) quantify spatial volumes in terms of "tetravolumes" and (b) dissect spatial volumes in terms of tetrahedral components. Most famously, he dissects the space-filling tri-rectangular tetrahedron, dubbed the Mite in his namespace (lexicon), into two "A modules" (a left and a right) and one "B module" (a left or a right). Given (a) -- the commitment to tetravolumes -- these two modules turn out to have a volume of 1/24, meaning the space-filling Mite has a volume of 1/8. This is the simplest space-filling shape without overt left or right handedness, hence the term Mite for Minimum Tetrahedron.
Synergetics: Explorations in the Geometry of Thinking was originally published in two volumes by Macmillan and is dedicated to H.S.M. Coxeter (with permission). The work was subsequently put on the Web by Dr. Robert Gray (with the permission of the estate).
Fuller received a Medal of Freedom from President Ronald Reagan, plus was the recipient of many honors and awards. His picture was on the cover of Time Magazine. That same picture was subsequently used by the United States Post Office for one of its stamps. Buckminsterfullerene, the third allotrope of carbon, was discovered subsequent to Fuller's death and was named in his honor.
These simple fractions and whole numbers have a streamlining effect, making the brand of spatial geometry less awkwardly intimidating to younger students, or so goes the advertising (I've found this to be true in my own geometry teaching).
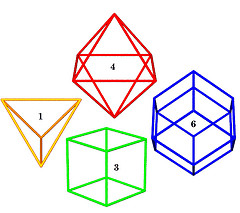
The context for his concentric hierarchy of angle-specified (pre-frequency) polyhedra is the sphere packing matrix known as the CCP or FCC in traditional nomenclature. Four closest packed balls define his unit volume tetrahedron, whereas the space-filling rhombic dodecahedral casement (voronoi cell) surrounding each of these spheres has a relative volume of six. His tendency to use the CCP as his native context attracted some attention from crystallographers (Dr. Arthur Loeb for example) as their discipline makes extensive use of this scaffolding.
Within his concentric hierarchy he defines a unifying dynamic transformation dubbed The Jitterbug which connects the lattice symmetries with five-fold rotational symmetry. The cuboctahedron and icosahedron have a special relationship in having the same number of surface points or unit-radius balls, as this transformation makes obvious. Fuller's many geodesic spheres owe a lot to such thinking.
Quadray Coordinates
David Chako, Gerald de Jong and Tom Ace did a lot of the heavy lifting, while I attempted to present their results in a readable and understandable set of "papers" (web pages). You might also call these Chakovian Coordinates.
They're similar to the barycentric coordinates, are especially relevant to those of us wanting to explicate Fuller's meaning of 4D, a third meaning which diverges from both Einstein's and H.S.M. Coxeter's (already two distinct meanings).
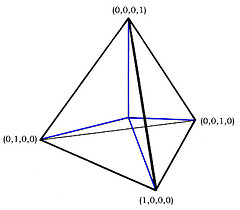
Quadray Coordinates abandon the notion of linear independence in favor of the four co-depending directions of any tetrahedron. A regular tetrahedron centered at the origin (0,0,0,0) has four radiating vectors of (1,0,0,0), (0,1,0,0), (0,0,1,0) and (0,0,0,1) respectively (think about left versus right handedness).
Therefore all points in space may be represented as the linear combination of these four, with every coordinate positive and at least one of them zero. An inside-out "through the looking glass space" making use of negatives might complement our Positive Universe (or world).
The effect of this apparatus is to divide space into four quadrants, in contrast to XYZ coordinates, which use the negative mirrors of the three positive unit vectors to carve space into eight octants.
In the namespace of XYZ, we think in terms of "three dimensions" at 90 degrees to one another and teach that these are conceptually separable, i.e. height with neither breadth nor width is considered a dimension all by its lonesome.
In the namespace of Quadrays, we consider the four directions to be conceptually irreducible in the sense that an observer or camera will always have a spatial relationship to any point, line or plane, ergo the dimensional context is an invariant.
In labeling volume (res extensa) 4D instead of 3D, we're taking our cues not only from Bucky (as he preferred to be called) but from dimension theorist Karl Menger who suggested a non-Euclidean "geometry of lumps" might someday find application. Given mathematics has room for multiple internally consistent ways of thinking, we have no reason to fear this unorthodox nomenclature.
Elastic Interval Geometry
Again, I was mostly an innocent bystander on this one. Karl Erickson and Russell Chu were early power users of Gerald de Jong's Struck program, which later morphed into Darwin at Home. Alan Ferguson gave us the lovely SpringDance application, written in Delphi, which some of us still use, while Tim Tyler provided Springie. All of this work owes plenty to Kenneth Snelson, a friend and one of Bucky Fuller's chief rivals in a tug-o-war over who invented Tensegrity, a word that continues to resonate with multiple meanings.
Web Resources
| Elastic Interval Geometry / Tensegrity |
Math Through Programming
Kenneth Iverson, Seymour Papert, Alan Kay and others pioneered the idea that mathematics learning could be usefully aided and abetted by a computer language. In the 1980s, when BASIC and Logo were sweeping the computer world, this looked like a promising trend. Many of us saw Guido van Rossum's Computer Programming for Everybody (CP4E) as another step along this road. I was invited to a meeting in London courtesy of The Shuttleworth Foundation to assist with some of the brainstorming in this direction.
I worked briefly with Kenneth on a short essay about the J language, which, like its predecessor APL, is a powerful mathematical tool. Alan Kay was at our London meeting, as was Guido. I've continued to promulgate Python as an accessible language for learning math concepts in a more object-oriented style. I have lots of essays on the web explaining exactly what that might look like.
I was invited to join the Python Software Foundation in March of this year. Maria Droujkova's Math 2.0 initiative had led me to start this WikiEducator project in hopes of further contributing to the free education movement.
Geometrical Studies
- David Koski and I both received a Synergetics Explorer Award from the Buckminster Fuller Institute back in the early 1990s. He was making original discoveries in connection with dissecting polyhedra into a minimal set of constituent tetrahedra, branching off from work done by Fuller around his so-called T-module, with the same volume as the A and B modules. David does the investigations and I provide some of the documentation.
- I worked with Steve Waterman on some of his early studies, suggesting we call the family of polyhedra he was studying Waterman Polyhedra. My experience with POV-Ray and Visual FoxPro enabled us to generate some early images.
- In November of 2001, Russell Chu, myself, Chris Fearnley, Ed Applewhite, Bonnie DeVarco and others help get SNEC off the ground, now known as the Synergetics Collaborative. We held a meeting in Washington, DC shortly after 911 to get the ball rolling.
- Stu Quimby and Cary Kittner also enlisted my talents as a programmer and graphic designer around their StrangeAttractors , a geometry toy. I still have one of the original shrink wrapped versions, a rarity given Design Science Toys was unable to stay in business.
- Anticipating that we might be moving beyond calculators in the math-learning classroom, I developed a number of Python modules based on my Beyond Flatland approach. A math-through-programming curriculum might take many forms, however today's software suggest a Renaissance in spatial geometry, especially around polyhedra, as a first order of business.
- Hypertoons: I originally shared this idea with Richard Hawkins in the mid-1990s but didn't have the programming power to actually implement the concept until more recently. A hypertoon links key frames (nodes) via a myriad of scenarios (edges) such that the viewer traverses a network of smooth transformations. The concept is not limited to pure geometry. David Scott Daniels, a computer scientist, worked with me on this project.
Web Resources
| Geometric Studies |
First Person Physics
Dr. Bob Fuller noticed my essay on First Person Physics, dealing with Bucky Fuller's concept of energy slaves, a way of adapting the concept of "horsepower" to a more contemporary mindset (few of us work with horses anymore). An "energy slave" is the equivalent of a human being in terms of work output, yet is a measure of the power of inanimate machinery, industrial scale processes, or perhaps of Nature herself. Teaching physics from a more first person perspective jibed with a more biomedical approach to the subject, as featured in textbooks by Dr. Urone.
Dr. Fuller assembled a team, including myself, and tried to get some NSF funding to run a pilot project. As a part of our collaboration, I used a ray tracer to convert sensor data from a ballerina, recorded as spreadsheets, into gracefully moving animated stick figures. The final CD was called Understanding Human Motion and was made available to physics teachers at a national conference, as a part of their registration packet. It was my privilege to accept an invitation to a meeting at the University of Nebraska at Lincoln in connection with this project.
Entrepreneurial
Coffee Shops Network
This project is about providing blueprints for a kind charitable giving involving computer game playing. Many states already use game playing in bars to raise funds. According to this model, the players themselves would receive credit for their record of philanthropic activity. One could still specify oneself, or the state government, as worthy beneficiaries, but those wouldn't be the only two options.
I've also been looking at ways to harness the sophisticated visual vocabulary of the Fuller network to advertise the humanitarian objectives of various commercial initiatives. This is where 4D Studios comes in, along with some other ideas for better business infrastructure around Portland, aimed at harnessing more of our collective power to generate both comic books and computer animations (cartoons, anime, manga).
The engineering community could use a makeover, given the misanthropic emphasis on "killingry". Livingry includes music and theater, as well as the visual arts. Project Renaissance is in the background on this one, as is General Systems Theory, a competitor with more traditional Economics.
Linus Pauling House
My social network includes a group calling itself Wanderers that meets in the boyhood home of the famous chemist Linus Pauling. The house is on a small campus of three buildings and could serve to anchor more charitable activities, were we able to attract a more international cast of sponsors to take our plans seriously. I'm on the board of the Institute for Science, Engineering and Public Policy, the non-profit which operates the facility.