ISO QUANT AND ISOCOST
| 
MICRO ECONOMICS
|
Isoquant and Isocost |
|
Introduction |
The focus of this chapter is on the firm. The chapter examines the theory of production or how firms organize production i.e. how it combines resources or inputs to produce final commodities. Production theory is extended to deal with two variable inputs by the introduction of isoquants. From the theory of production where only one or two inputs are variable, we proceed to examine cases in which all inputs are variable.
|
Learning Objectives |
After reading this chapter, you are expected to learn about:
While going through this analysis students may feel it is a revision of the indifference curve and the budget line. Isocost and isoquants play the same role in producer’s equilibrium as that played by the budget line and indifference curves in consumer’s equilibrium. Isocost curve is a producer’s budget line while isoquant is his indifference curve. | |
 |
Definition |
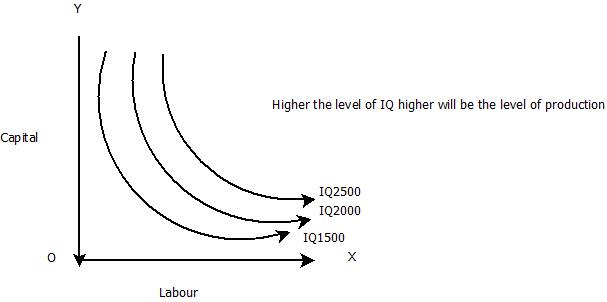
Isoquant is also called as equal product curve or production indifference curve or constant product curve.
Isoquant indicates various combinations of two factors of production which give the same level of output per unit of time. The significance of factors of productive resources is that, any two factors are substitutable e.g. labour is substitutable for capital and vice versa. No two factors are perfect substitutes. This indicates that one factor can be used a little more and other factor a little less, without changing the level of output.
It is a graphical representation of various combinations of inputs say Labour(L) and capital (K) which give an equal level of output per unit of time. Output produced by different combinations of L and K is say, Q, then Q=f (L, K). Just as we demonstrate the MRSxy in respect of indifference curves through hypothetical data, we demonstrate the Marginal Rate of Technical Substitution of factor L for K (MRTS L,K )
| |
Assumptions |
- There are two factor inputs labour and capital
- The proportions of factor are variable.
- Physical production conditions are given
- The Scale of operation is variable
- The state of technology remains constant
The shape of Isoquant
In this section we examine the characteristics of isoquants, define the economic region of production and consider the special cases where the commodities can only be produced with least cost factor combination.
We can see that the shape of isoquant plays an important a role in the production theory as the shape of indifference curve in the consumption theory. Iso quant map shows all the possible combinations of labour and capital that can produce different levels of output. The iso quant closer to the origin indicates a lower level of output. The slope of iso quant is indicated as [math]\frac{K}{L}[/math]=MRSLk=[math]\frac{MPL}{MPk}[/math]
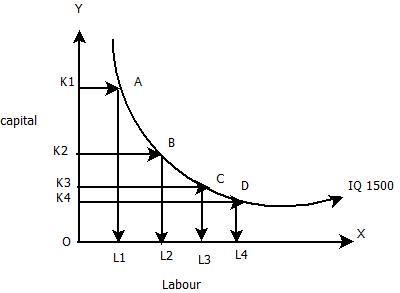
Table indicating various combinations of Labour and Capital to produce 1500 Units of Output
| COMBINATIONS | UNITS OF CAPITAL | UNITS OF LABOUR | TOTAL OUTPUT |
|---|---|---|---|
| A | 50(OK) | 1 (OL1) | 1500(IQ1) |
| B | 45(OK2) | 2(OL2) | 1500(IQ1) |
| C | 41(OK3) | 3(OL3) | 1500(IQ1) |
| D | 38(OK4) | 4(OL4) | 1500(IQ1) |
| |
Properties/Characteristics of Isoquants |
Isoquants, abbreviated as IQs, possess the same properties as those of the indifference curves. For the convenience of the students, we can state them as follows.
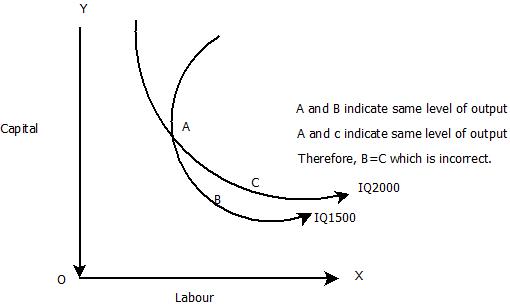
- Two isoquants do not intersect each other:
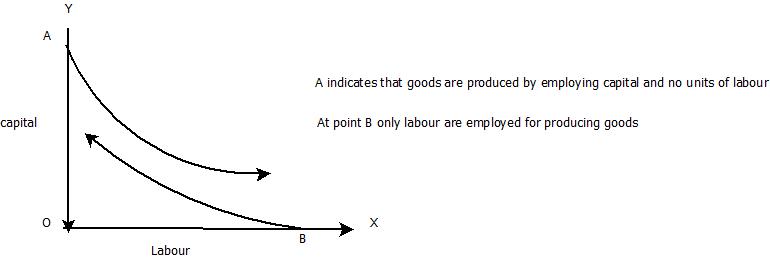
- No isoquant can touch either axis
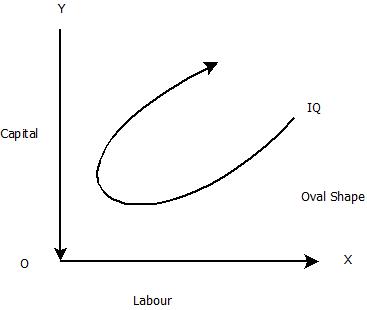
- Isoquant is oval in shape
- A higher IQ implies a higher level of output
- IQs are never parallel to each other. Interspacing between them is least at the ends and maximum in the middle.
- IQs are convex to the origin: convex isoquants possess continuous substitutability of K and L over a stretch. Beyond this stretch, K and L are not substitutable foe each other.
- IQs may be linear when labour and capital are perfect substitute. A linear isoquant implies that either factor can be used in proportion. If isoquant has several linear segments separated by kinks, the isoquant is called kinked isoquant or activity analysis isoquant or linear programming isoquant. Such isoquants are used in linear programming.
- If Land K are prefect complements to each other, the IQ is L-shaped. Such isoquant is known a input-output isoquant or Leontief isoquant. There is only one combination of L and K available for production. It is the corner point of L-shaped isoquant.
- If marginal product of one of the two factors is zero, IQ is parallel to the axis on which the factor with zero marginal products is represented.
- If one of the two factors has negative marginal product the IQ slopes upwards from left to right.
- If both the factors have negative marginal products, the IQ is concave to the origin.
- If the producer has a preference for a factor of production, the IQ is quasi linear.
- If the factors to be employed in whole numbers units only. The IQ is discontinuous.
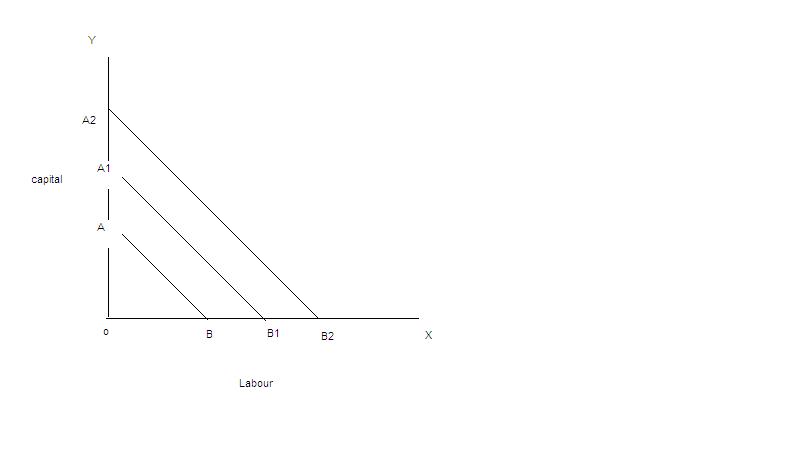
Isocost curves:
Isocost curve is the locus traced out by various combinations of L and K, each of which costs the producer the same amount of money (C ) Differentiating equation with respect to L, we have dK/dL = -w/r This gives the slope of the producer’s budget line (isocost curve). Iso cost line shows various combinations of labour and capital that the firm can buy for a given factor prices. The slope of iso cost line = PL/Pk. In this equation , PL is the price of labour and Pk is the price of capital. The slope of iso cost line indicates the ratio of the factor prices. A set of isocost lines can be drawn for different levels of factor prices, or different sums of money. The iso cost line will shift to the right when money spent on factors increases or firm could buy more as the factor prices are given.
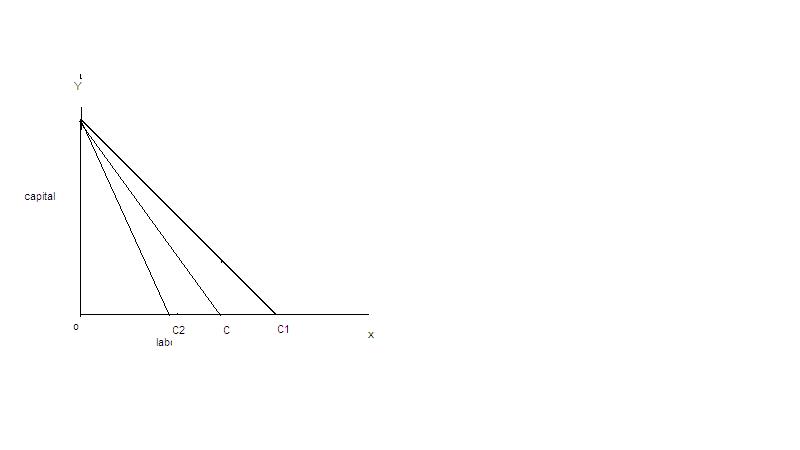
Slope of iso cost line
With the change in the factor prices the slope of iso cost lien will change. If the price of labour falls the firm could buy more of labour and the line will shift away from the origin. The slope depends on the prices of factors of production and the amount of money which the firm spends on the factors. When the amount of money spent by the firm changes, the isocost line may shift but its slope remains the same. A change in factor price makes changes in the slope of isocost lines as shown in the figure.
Least Cost Factor Combination or Producer’s Equilibrium or Optimal Combination of Inputs
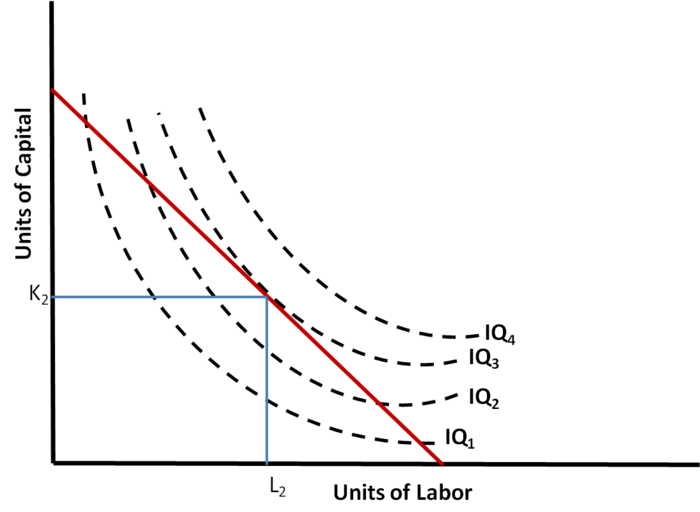
The firm can achieve maximum profits by choosing that combination of factors which will cost it the least. The choice is based on the prices of factors of production at a particular time. The firm can maximize its profits either by maximizing the level of output for a given cost or by minimizing the cost of producing a given output. In both cases the factors will have to be employed in optimal combination at which the cost of production will be minimum. The least cost factor combination can be determined by imposing the isoquant map on isocost line. The point of tangency between the isocost and an isoquant is an important but not a necessary condition for producer’s equilibrium. The essential condition is that the slope of the isocost line must equal the slope of the isoquant. Thus at a point of equilibrium marginal physical productivities of the two factors must be equal the ratio of their prices. The marginal physical product per rupee of one factor must be equal to tht of the other factor. And isoquant must be convex to the origin. The marginal rate of technical substitution of labour for capital must be diminishing at the point of equilibrium.
The Economic region of production
The firm would not operate on the positively sloped portion of an isoquant because it could produce the same level of quantity with less capital and labour. Economic region of Production:
Ridge lines: separate the relevant (i.e. negatively sloped) from the irrelevant (or the positively sloped) portion of the isoquant.
Ridge lines joins points on the various isoquants where the isoquants have zero slope (and thus zero MRTSlk) .
| Enter your text here |
|
Activity |
| Write your activity here | |
| Example: {{{Example}}} |
|
|
Self-Assessment Questions (SAQs) {{{n}}} |
| {{{SAQ}}} | |
|
|
|
Results |
An isoquant shows the various combination of two inputs that can be used to produce a specific level of output. From the isoquant map, we can generate the total product curve of each input by holding the quantity of the other input constant.
Isoquants are negatively sloped in the economically relevant range, convex to the origin and do not intersect. The absolute value of the slope of Isoquant is called the Marginal Rate of Technical Substitution. This equals the ratio of marginal productivity of two inputs.
As we move down along an isoquant the absolute value of its slope or Marginal Rate of Technical Substitution declines and the isoquant is convex. Ridge lines separate the relevant (i.e. the negatively sloped) from the irrelevant (or positively sloped) portion of the isoquant.
With right angled or L shaped, isoquant , inputs can only be combined in fixed proportion in production.
|
Key Terms |
Iso Quant
Iso cost
Ridge Lines
Least Cost Combination
Producers Equilibrium
Marginal Rate of Technical Substitution
| Enter your text here
|
|
References and Bibliography |
- Principles of Microeconomics,Dominick Salvatore Fifth Edition, Oxford International Student Edition.
- Micro Economics:Edwin Mansfield and Gary Yohe,Tenth Edition, Published by W.W. Norton & Company
- Economics:Samuelson and Nordhaus,Eighteenth Edition, Published by Tata McGraw Hill
|
|
Further Readings |
