FreeEnergyLesson2
Contents
LESSON 2
GIBBS ENERGY OF FORMATION, GIBBS ENERGY OF REACTION
Similarly as for internal energy, U, and for enthalpy, H, it is in principle not possible to find an solute value of G for a system. One can only find changes in Gibbs energy. By convention the bbs energy of formation refers to the formation of one mole of the co mpound from the elements their most stable state at a given temperature and pressure. The Gibbs energy of formation is given ~ symbol Δ f G. This convention corresponds perfectly to the convention for Δ f H., see section 4.4. In tables one usually finds values referring to a temperature of 25°C or 298 K and a pressure of 1 bar (or to 1 atm in older tables). These values are given the symbol Δ f G° 298 . and are called standard Gibbs energies of formation. It follows from this convention that the standard Gibbs energy of rmation is equal to zero for an element in its most stable state.
We can find the value of the standard Gibbs energy of formation for a compound when the lrresponding values are known for the standard enthalpy of formation and for the standard absolute ltropies of the compound and the elements. From eq. (6.9) we obtain for any reaction at constant T:
Δ r G = Δ r H - TΔ r S (2.1)
Example 1
As an example we may calculate the value of Δ f G° 298 . for liquid water. From table 4.1 we find Δ f H° 298 . for liquid water:
H 2 (g) + 1/2 0 2 (g) → H 2 (I) Δ f H° 298 . = - 286 kJ mol-1
Since entropy is a state function, entropy values are additive in the same way as enthalpy values:
Δ f S = ∑V i S i (2.2)
where VI are stoichiometric coefficients in the chemical equation for the fOrmation of one mole of the compound from the elements. From table 5.2 we find the following valued for absolute entropies, given in the units
J mol-1 K-1 S° 298 (H 2 ,g) = 131 , S° 298 (O 2 ,g) = 205, S° 298 (H 2 0,l) = 70.
Thus the standard entropy of formation for liquid water, Δ f S° 298 will be:
Δ f S° 298 = - 131 - 1/2 x 205 + 70 = - 163.5 1 J mol-1 K-1
Δ f G° 298 = Δ f H° 298 - TΔ f S° 298 = - 286 - 298 x (-163.5/1000) = - 237 kJ mol-1
(Watch the units. In tables one usually finds ΔG° and ΔH° values given in kilo joule, while S° and C p ° values are given in joule K-1.)
Example 2
In a similar way we may find the value of Δ r G° 298 for the chemical reaction
CO (g) + 1/2 0 2 (g) → CO f (g) Δ r G° 298
We have already found Δ r H° 298 = - 283 kJ for this reaction, section 4.4. Using values from table 5.2 for S° 298 , we find for this reaction Δ r S° 298 = 214 - 198 - 1/2 x 205 = - 86.5 1 K-1 and thus
Δ r G° 298 = Δ r H° 298 - TΔ r S° 298 = - 283 - 298 x (- 86.5/1000) = - 257 kJ
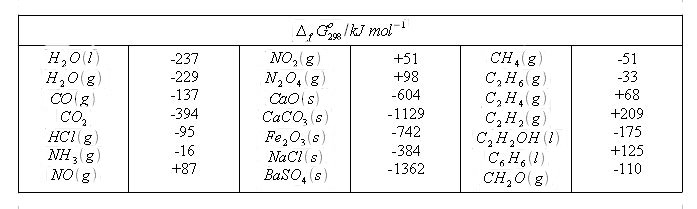
Table 2.1 gives standard Gibbs energies of formation for some different compounds. The values have been Calculated in the same way as the value for liquid water above.
The Gibbs energy is a state function, and thus the values are additive in the same way as enthalpy values and entropy values. The standard Gibbs eneergy for a reaction, Δ r G° 298, is equal to the sum of Δ f G° 298, values for the products minus the sum of Δ f G° 298 values for the reactants:
Δ r G° 298 = ∑ i V i Δ f G° 298 (2.3)
where V i are the stoichiometric coefficients in the chemical equation.
Example 3
Thus we can calculate Δ r G° 298 for the chemical reaction studied above, directly from values given in Table 6.1:
CO (g) + 1/2 O 2 (g) → CO 2 (g)
Δ r G° 298 = - (- 137) - 0 + ( - 394) = - 257 kJ
From the sign for Δ r G° 298 we obtain valuable information about the chemical reaction. When Δ r G° 298 is negative, as in the example above, we will know that there will be a spontaneous reaction from left to right when reactants and products are in standard state. When Δ r G° 298 is positive, the reaction will be spontaneous from right to left. (Only very rarely one finds Δ r G° 298 = 0)