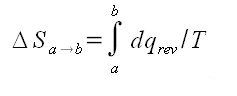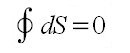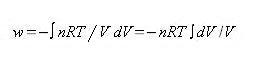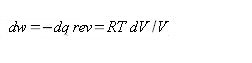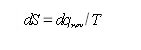EntropyLesson1

LESSON 1: ENTROPY IN CHEMICAL THERMODYNAMICS

Spontaneous Processes and Entropy

Learning Outcomes

As a result of learning this topic learners should be able to:

• Explain the meaning of the term Spontaneous Change as it applies to physical and Chemical reactions
• Identify Spontaneous physical and chemical Processes.
• Understand relationship between spontaneous reactions and probability and hence entropy

Our experiences tell us that certain processes will always occur without assistance from an external action. such processes which occur in a system left to itself and given enough time with no external intervention is known as a spontaneous process It is important at this point to recognize the most important feature of a spontaneous process that is it has a definite direction in which it occurs. Consider a familiar example where an egg is dropped' it spontaneously break on impact with a hard surface. The reverse reaction in which the broken egg shells rise from the floor and reassemble themselves is unconceivable and cannot happen. Such a reverse reaction is non spontaneous. A process that is spontaneous in one direction is non spontaneous in the opposite direction. Consider the following physical and chemical processes as a way of looking and identifying spontaneous processes.

Fig 1.1 A gas expanding in a vacuum

• A gas expanding into a vacuum as illustrated in Figure 1.1. We see this happen but not the reverse process of a gas compressing itself spontaneously into the left part container
• We measure heat flowing from a hot body to a cold one when they are brought into thermal contact, but never detect heating flowing spontaneously in the reverse direction as indicated in Fig 1.2 below.We know what would happen- the temperature of each block will change until the two blocks reach uniform intermediate temperature. There is a spontaneous flow of heat from the hot block to the cold block. It is inconceivable that the two blocks at the same temperature can be found to at any other temperature unless an external influence acts on the two.
• A waterfall runs downhill but never up spontaneously
• A lump of sugar spontaneously dissolves in a cup of tea but dissolved sugar does not spontaneously reappear in the original form.
• Iron exposed to water and oxygen forms rust but rust does not spontaneously change to iron

Fig 1.2 Spontaneous heat flow in ice cubes

Fig 1.3 Spontaneous flow of water from a water fall

Fig 1.5 An iron nail exposed to water and oxygen

Fig 1.4 A lump of sugar dissolving spontaneously in a cup

From these examples we might draw the following conclusions:

• If a process is found to be spontaneous, the reverse process is nonspontaneous
• Both spontaneous and nonspontaneous processes are possible but only spontaneous process will occur naturally. Non spontaneous processes require the system to be acted upon in some way.

One of the main objectives in studying thermodynamics is to predict whether not a certain reaction will occur when reactants are brought together under special sets of conditions ( at certain temperature, pressure or concentration). In other words thermodynamics principles can be used to answer the question “Does a particular Chemical Reaction spontaneously proceed in the forward direction?”

We introduce a new state fn, entropy and show how examining changes in entropy can lead to a general predictions about the direction of spontaneous change and the nature fo the equilibrium state that is ultimately achieved. We explore the connection between entropy, macroscopic property and the extent of disorder present on an atomic scale .

We then consider another state function, the Gibbs free energy and demonstrate its connection to entropy and enthalpy in chemical reactions

This lesson focuses on how these two important thermodynamic quantities, entropy and free energy are used to answer the above question.

Fig 1.6 Free Energy illustrate through a downcase fall

Before we answer the question is there a thermodynamic quantity that can help us predict whether a process will occur spontaneously? It is logical to assume that spontaneous processes occur so as to decrease the potential energy of the system.This assumption helps tp explain why things fall downcase and why springs in a clock unwind.

In chemical reactions, too, we find that a large number of exothermic reactions are spontaneous but so are some endothermic ones. e.g the melting of ice at room temperature.

(1.1)

As another example, consider the croling that results when ammonium nitrate dissolves in wate

(1.2)

The dissolution process is spontaneous, yet it is also endothermic

In abandoning enthalpy as our criterion for spontaneous change, let us agree that there is need to look for another thermodynamic quantity (in addition to enthalpy) to help predict the direction of a chemical reaction. Thus quantity is called entropy which we will consider in the next topic

An important part of chemistry is concerned with the state of equilibrium and the tendency of a system to move in the direction of equilibrium. The second law of thermodynamics is concerned with the direction of spontaneous reactions and with equilibrium. Since both exothermic and endothermic reactions may proceed spontaneously, the driving force of a chemical reaction cannot be explained by the change in enthalpy alone. A process that occurs spontaneously involves a change from a state of lower probability to a state of higher probability. Entropy is a measure of probability.

The change in entropy from a state a to a state b is defined:

(1.3)

The Carnot cycle is used to show that entropy is a state function, that the change in entropy for a cyclic process is zero:

(1.4)

The entropy change for a system is accompanied by an entropy change in the surroundings. For a reversible process, these two entropy changes balance, and the total entropy change is zero. For an irreversible process (a spontaneous process) the total entropy change is positive.

There are no absolute values for internal energy, U and enthalpy, H. The entropies, however, have absolute values. The third law of thermodynamics states that the entropy is equal to zero for a perfect crystal at zero Kelvin. This makes it possible to calculate absolute values for the entropy. Absolute values for entropy are given in tables.

Spontaneous Reactions and Probability

Changes in internal energy or in enthalpy of a system are not suitable indication of the tendency of a reaction to proceed in a given direction. Experimentally one has found that both exothermic reactions (∆H < 0) and endothermic reactions (∆H > 0) may proceed spontaneously. Thus the driving force of a chemical reaction cannot be explained by the value of ∆H alone.

There are also physical processes which have a preferred spontaneous direction that cannot be explained on the basis of the first law of thermodynamics alone. An ideal gas expands spontaneously into an evacuated container. According to Joules experiment there is no change in internal energy nor in enthalpy upon the expansion. The reverse process - a spontaneous collection of gas molecules in only a part of the total volume available never occurs. Another example: You know from your experience that heat flows spontaneously from a hot to a cold body, but never from a cold to a hot body.

The second law of thermodynamics is concerned with the direction of spontaneous reactions and with equilibrium. It can be stated in many ways, one formulation is: Every system that is left to itself will, on the average, change toward a condition of maximum probability.

The expansion of an ideal gas to fill the total volume available is perhaps the most easily conceived example of the second law. When molecules move about at random speeds in random directions, they will, at any moment, most probably be evenly distributed throughout the container. By chance there will momentarily be very, very small fluctuations in distribution. The equilibrium distribution, however, will quickly restore itself, and the chance of all molecules collecting in one part of the volume is virtually nil. The equilibrium is dynamic:, and the process taking place is reversible. The state functions of the system never change by more than an infinitesimal amount from one moment to another. In Joule's experiment the ideal gas expands into an empty volume. This can be described as a process going from low to high probability. A distribution of the gas molecules giving the same pressure in the two volumes is the most probable distribution.

The Entropy of an Ideal Gas

Let us first remind ourselves about the first Law of Thermodynamics . The first law is a statement on the conservation of energy .

Fig 1.7 A state function

The first law states that the internal energy of a system is property of the system ( a state function ) , and that changes in the internal energy , dU , results from the sum of energy added in the form of heat , dq and work,dw

dU=dq+dw (1.5)

Let us now consider the reversible expansion of an ideal gas from one state to another at constant temperature and against an external pressure , P_ex .In this case the there will be a change of volume from initial state V ₁ to volume V₂.

Fig 1.8 Reversible expansion of an ideal gas against external pressure

The work supplied to the system , dw , is negative

dw = -force X dl = -P_exAdl = -P_exdV (1.6)

wheredV is the change in volume . For a reversible process P_ex =P_in

we can therefore write dw =- P_indV or just

dw =-PdV (1.7)

During an isothermal expansion the internal pressure will decrease. If we adjust the external pressure to very close to the internal pressure all the time ( by removing small weights as shown in Fig1.8, ( one by one ) , the integral work supplied will be

(1.8)

In order to keep the temperature constant heat must be supplied to the system during the expansion.

If the system is an ideal gas (PV=nRT) and we have for the work expression above

(1.9)

Where V₁ and V₂ are the initial and final volume respectively.

Coming back now to consider the entropy change for reversible expansion of the gas. For an isothermal expansion

for one mole of gas.

At constant temperature q_rev. is a function of volume V only.

We shall now define a new quantity , the entropy :

(1.10)

for an isothermal expansion of the ideal gas from V₁ to V₂ we have

(1.11)

For n moles of gas:

(1.12)

Then the entropy change is given the volumes in the final and initial states. It does not depend on the path taken between the to states.

It is good to note that this example we have gone through of reversible expansion of an ideal gas is not a sufficient proof that entropy is a state function.

To show entropy is a state function we must prove that the total change in the entropy of a system is zero for any cyclic process.

∫ dV = 0. This will be done in Lesson No 2.

Calculation of change in entropy in a reversible expansion of ideal gas at constant temperature.

A sample of an ideal gas is confined to a cylinder fitted with piston of 5 cubic centimeter. It occupies 500 cubic centimeter and at room temperature it exerts a pressure of 2 atmospheres. What is the change of entropy of the gas when the piston is withdrawn isothermally through 100cm ?

Since this is an ideal gas , we can calculate the amount of gas Using the relationship

(1.13)

N = ( 2 atm) x ( 5x10-4 m3)(/0.082dm3 atm.K¬_1 mol-1)x298 = .041 mol

∆S = (0.041 mol) x (8.314JK_1mol_1) ln (1000/500) = (0.34JK_1) ln 2 = .024 Jk_1

It is helpful to remember that the dimensions of entropy , S , the same as those both of , R ,and heat capacity , C .

NB. The limitations of this calculation should be appreciated. The calculation is applicable to an ideal gas because he dispersal of the energy was identified with spatial dispersal of the atoms. This is only possible when one ascribes energy to individual particles. The calculation would be more complex when the particles interact with each other. Then their energy would depend on their separation. It is also more complex when when particles can rotate and vibrate.

Revision

Some fundamental Equations

Exercise

1. Read more on the concept of entropy from statistical point of view and explain why Entropy is usually called the “arrow of time “.see pages 56 5.1 5.2 5.11 5.9
2. One mole of an ideal gas goes from state I : P1 =5 bar , T1 =300K to state P3 , T3 = 200K . The final state can be reached by a reversible isothermal expansion to a pressure P2 (state 2 ) , followed by a reversible adiabatic expansion to state 3. Calculate the entropy change for the gas , ∆S system for the process from state 1 to 3