Systems Approach

MEASURE D: Systems Approach

The final FTE method that will be discussed here is based on a combination of input and output measures. Essentially, each phase or cycle of education is conceived of as a closed system, with inputs (in terms of subject/course years of study and the costs incurred) and outputs (in terms of examination subject passes). The Systems Approach establishes the productivity factor for conventional education (total outputs ÷ total inputs) and uses this to calculate what the equivalent number of ODL learners would be to maintain the same level of productivity. The Systems Approach is the most comprehensive method of establishing FTE and, arguably, the fairest.

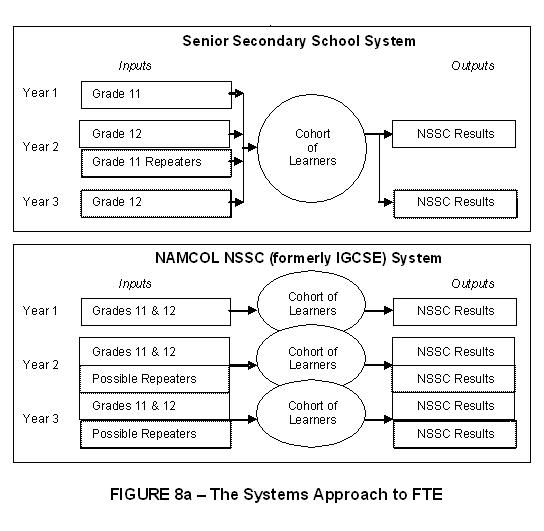
The difficulty in establishing equivalency lies in the fact that learners in the conventional education system often receive inputs for a number of years before any outputs are realised. By way of contrast, those studying with an ODL institution usually produce outputs after only a single academic year of inputs. The concept underlying the Systems Approach is illustrated in Figure 8a below, which compares senior secondary courses offered by the Namibian College of Open Learning (NAMCOL) with those provided in conventional schools in Namibia.

Ideally, we should trace the progress of a single cohort of school-based learners through Grades 11 and 12. Most of these learners will complete the senior secondary phase of their education within a period of two years, but a small number will be allowed to repeat Grade 11. Thus, between two and three years of inputs are required for each learner in the senior secondary phase of the formal education system in order to produce a single set of outputs, measured in terms of the NSSC (Namibian Senior Secondary Certificate) examination results. It is only at the end of Year Two and Year Three that the outputs achieved by this cohort can be measured. We need to add up the number of learners in Grade 12 in the current year and the number in Grade 11 in the previous year to obtain the total inputs, expressed in terms of student years of study. In this example, the repetition rate for Grade 11 in Namibia is extremely low (less than 2%), so it can be conveniently ignored. Where repetition rates within a particular phase of education are higher, it may be necessary to modify the calculation in order to take this into account.

As shown in Figure 8a, the inputs received in a single year by the cohort of NAMCOL students are equivalent to two years of inputs in conventional schools. This is because the study materials provided to the College’s learners cover the curricula for both Grade 11 and Grade 12. The unit for measuring these inputs is a subject enrolment. At the end of the same academic year, each cohort produces a set of outputs, measured in terms of subject passes. A student who fails the examination and wishes to repeat must register for the same subject the following year. Because those who make up the NAMCOL cohort change from year to year, it is extremely difficult to trace the progress of individual learners and tally their cumulative results. Thus, the inputs and outputs for a single academic year are used for comparison.

STEPS in applying the Method:

a. Identify the total number of examination subject passes by full-time students at the end of the school year in question.

b. Identify the total number of full-time students who completed the final year of the cycle/phase (e.g. junior secondary, senior secondary, certificate, diploma, etc.) during the school year in question.

c. Identify the total number of full-time students enrolled during the next previous year and so forth for each year in the cycle/phase.

d. Add together the values obtained for Steps b and c.

e. Divide the figure from Step a by answer obtained in Step d. This is the productivity ratio for conventional education.

f. Divide the total number of examination subject passes for ODL students by the result of Step e.

EQUATION:

FTE_SA = TESP_ODL ÷ (TESP_FT / (TSF_FT+ TS_FT-1 + TS_FT-2. . .))

Where:

FTE_SA = FTE Measure D: Systems Approach

TESP_ODL = Total Examination Subject Passes by ODL students in current year

TESP_FT = Total Examination Subject Passes by Full-Time students in current year

TS_FT = Total number of Full-Time Students in current year

TSF_FT-1 = Total number of Full-Time Students in previous year

TS_FT-2 = Total number of Full-Time Students in the next previous year

Activity

Exercise 8.4 You can try out the Systems Approach for calculating FTE student numbers by carrying out Exercise 8.4. Feedback: Check your calculations by clicking on Exercise 8.4 - Answer Sheet.

The principal argument in support of the Systems Approach is that it is based on what is actually invested (inputs) and what is actually realised (outputs) in both conventional education and ODL programmes. The calculation also takes account of differences in credit- or work-loads, duration of courses and drop-out rates.

One possible drawback of the Systems Approach is that it requires reliable figures for both school enrolments (over a number of years) and examination results. These may not always be easy to obtain, though most Education Ministries collect and publish such statistics. In some countries, repetition rates are relatively high in conventional schools, particularly during the junior secondary cycle. This means that students who repeat of year in school receive additional inputs, which introduces a distortion in the calculation of FTE. Likewise, where students fail the examination in a particular subject after several years of formal education and then go on to pass the examination after a year of study in an open school, this has the effect of unfairly inflating FTE student numbers for ODL. In addition, the arguments in relation to student ability and starting levels outlined in Section 8.4 above are also relevant when critiquing the Systems Approach.