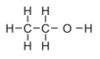Chemistry/The Density and Volume of a Water-Alcohol Mixture
INTRODUCTION
The purpose of this investigation is to discover
- the relationship between the density of a substance and the slope of a graph that shows the mass of the substance versus its volume, and
- what happens to the volume of an alcohol–water mixture as the relative volumes of water and alcohol are changed.
In addition, the investigation gives you practice in
- making accurate measurements of volume and masses, and
- construction and use of graphs involving experimental results.
Note: You are required to hand in your written report on a separate sheet of paper. This lab hand–out may be attached if you do not wish to re–copy the data tables. In this case, make sure your report mentions where the data is.
DATA
| Water | Alcohol | Mixture | ||||
|---|---|---|---|---|---|---|
| TRIAL | volume (mL) | mass (g) | volume (mL) | mass (g) | volume (mL) | mass (g) |
| 1 | 0.0 | ------ | 25.0 | 25.0 | ||
| 2 | 5.0 | 20.0 | ||||
| 3 | 10.0 | 15.0 | ||||
| 4 | 15.0 | 10.0 | ||||
| 5 | 20.0 | 5.0 | ||||
| 6 | 25.0 | 0.0 | ------ | 25.0 | ||
| column 1 | column 2 | column 3 | column 4 | |||
EXPERIMENTAL PROCEDURE
- Note: All masses MUST be recorded to 2 decimal places (0.01 g).
- All volumes MUST be recorded to 1 decimal place (0.1 mL).
- Whenever instructions refer to a “column” of data, you can find the column number at the bottom of the appropriate table.
- Note: All masses MUST be recorded to 2 decimal places (0.01 g).
1. Using a grease pencil, label one 25 mL graduated cylinder “A” (for Alcohol) and a second cylinder “W” (for Water). Wash and scrub the cylinders to clean them. Flick the cylinders several times to “shake them dry” and dry the outside of the cylinders. Weigh the empty cylinders and record the data in the DATA section.
2. Perform six sets of measurements as follows and record the results in Table 1. If a volume required is “0.0”, simply measure out the other liquid and continue. For each trial (HORIZONTAL line) in the Table perform parts 2(a) to 2(c) of this experimental step.
- (a) Flick the “water” cylinder several times to shake it dry and dry the outside of the cylinder. Then ACCURATELY measure the volume of water required (use a dropping pipette to be sure that the bottom of the water’s meniscus line just touches the required volume marking). After adding the water, weigh the cylinder and water and enter the data in column 1 of Table 1. Keep the water in the cylinder for use in part 2(c).
- (b) Flick the "alcohol" cylinder several times to dry it. Dry the outside of the cylinder. Then ACCURATELY measure the required volume of alcohol . Again, use a dropping pipet to be sure the alcohol’s meniscus line touches the volume marking. After adding the alcohol, weigh the cylinder and alcohol and enter the data in column 2 of Table I. Keep the alcohol for part 2(c).
- (c) Carefully, WITHOUT LOSING ANY LIQUID, mix the water and alcohol back and forth, FINALLY HAVING THE MIXTURE END UP IN THE ALCOHOL CYLINDER. Let the last of the mixture drain from the water cylinder into the alcohol cylinder for about 15 seconds. (In order to correctly analyze the data, the mixture MUST end up in one cylinder all the time and we are arbitrarily choosing to use the ALCOHOL CYLINDER for measurements on the mixture.) Then measure
- the volume of the mixture to the nearest 0.1 mL. Enter the volume in column 3 of Table I.
- the mass of the alcohol cylinder and mixture to 0.01 g. Enter the mass in column 4 of Table
Finally, discard the mixture down the sink.
ANALYSIS OF DATA
1. Fill in Table 2 as follows.
Column 1 (mass of water)
Calculate the mass of water used in each trial by subtracting the Mass of empty “water” graduated cylinder (recorded at the start of the DATA section) from each entry in column 1 of Table 1. DO NOT CHANGE THE VALUES IN TABLE 1. Enter the results in the corresponding space in column 1 of Table 2.
Column 2 (mass of alcohol)
For each trial, subtract the Mass of empty “alcohol” graduated cylinder from each entry in column 2 of Table 1. Enter the results in column 2 of Table 2.
Column 3 (volume of mixture)
Copy, unchanged, each entry from column 3 of Table 1 to column 3 of Table 2.
Column 4 (mass of mixture)
For each trial, subtract the Mass of empty “alcohol” graduated cylinder from each entry in column 4 of Table 1. Enter the results in column 4 of Table 2.
Column 5 (the sum of the masses of water and alcohol in each mixture)
For each trial, add the mass of water in column 1 of Table 2 to the mass of alcohol in column 2 of Table 2 for each trial. Enter the results in column 5 of Table 2.
Column 6 (the mass lost during the mixing process)
For each trial, subtract the mass of the mixture (column 4 in Table 2) from the combined mass given in column 5 of Table 2. Enter the results in column 6 of Table 2. [The entries in column 5 should be very close to the values in column 4. Column 6 tells us how much mass is lost by being left behind in the water cylinder (or by spillage) when the alcohol and water are mixed and poured back into the alcohol cylinder. Columns 5 and 6 are not used for calculations. Instead, columns 5 and 6 serve as a check on how carefully you carried out the experiment.]
Table 2: Mass (m) and Volume (V) for water, alcohol and a water–alcohol mixture
| Water | Alcohol | Mixture | mass water + |
sum – | ||||
|---|---|---|---|---|---|---|---|---|
| TRIAL | V ( mL) | m (g) | V ( mL) | m (g) | V ( mL) | m (g) | ||
| 1 | 0.0 | –––– | 25.0 | 25.0 | ||||
| 2 | 5.0 | 20.0 | ||||||
| 3 | 10.0 | 15.0 | ||||||
| 4 | 15.0 | 10.0 | ||||||
| 5 | 20.0 | 5.0 | ||||||
| 6 | 25.0 | 0.0 | –––– | 25.0 | ||||
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |||
2. Plot a graph of mass of water (vertical axis) versus volume of water (horizontal axis). Your graph
- must NOT be generated on a computer
- must have an easy–to–read scale (avoid scales such as “3 cm = 5 g”)
- must have easily–seen data points plotted (a small circle around the data point is excellent)
- must have properly labelled axes, including an indication of the units used
- must have a title which describes what is being plotted on the graph
- must have a SINGLE STRAIGHT LINE drawn, such that the line either goes through as many of the data points as possible OR has as many data points on one side of the line as there are on the other side. Don’t play “connect the dots” by using a series of straight–line segments. Don’t make the line go through the origin if the origin doesn’t lie on your line.
3. Read TWO POINTS from your “best” straight line and use the points to calculate the slope of the line. State the coordinates of the points used. Do NOT use experimental data points UNLESS they happen to lie on the line by coincidence. The points chosen MUSTbe as far apart as possible. Recall that if the points on a line are (x1 , y1) and (x2 , y2), then
Calculate the slope and express its value in decimal form. According to your graph, what are the units of the y–axis values and of the x-axis values? What are the derived units of the slope you calculated?
4. Plot a graph of mass of alcohol (vertical axis) versus volume of alcohol used (horizontal axis). Make sure that the graph is properly prepared, following the guidelines stated in analysis step 2, above.
5. Calculate the slope of the alcohol graph, expressing your answer in decimal form and indicate the units of the slope. (Don't forget to state the coordinates of the points used to obtain the slope.)
6. Use your graph for alcohol to find the mass of 12.5 mL of alcohol. Indicate clearly on your graph how the mass of 12.5 mL of alcohol is found.
7. Use the density equation ( d = m/V ) and your experimentally–found mass of 25.0 mL of water to calculate the density of water. (Don't forget to include the units for your calculated density.) Similarly, use your experimentally–found mass of 25.0 mL of alcohol to calculate the density of alcohol.
8. Suggest a reason why the numerical values found for the densities in analysis step 7 are so similar to the numerical values found for the slopes found in analysis steps 3 and 5. Note: this is a very important question and a major part of the purpose of this experiment.
9. You should have noticed that the MIXTURES all have a volume which is less than 25.0 mL (as shown in column 3 of Table 2). This decrease in volume is REAL, not an error in your experimental technique. (Column 6 of Table 2 should show you that very little mass and therefore very little volume of the mixture was “lost” during the mixing process.) The purpose of this question is to allow you to form a hypothesis that explains the decrease in volume occurring when water and alcohol are mixed.
- (a) Assume you have a 50 L barrel full of basketballs and a 50 L barrel full of tennis balls. If you dump both barrels full of balls into a 100 L barrel, will the 100 L barrel be full? Explain your answer.
- (b) Water is a small molecule consisting of 3 atoms joined together as shown below.
Alcohol is a large molecule consisting of 9 atoms joined together as shown below.
Using this information and the ideas in step 9 (a), make a hypothesis that explains the decreased volumes found for the mixtures in column 3 of Table 2.