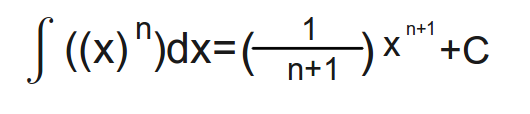Albany Senior High School/Tutorial Level 3 Calculus
Contents
Tutorial Level 3 Calculus
Polynomials and exponential functions
Trigonometric functions
Substitution
Definite Integration and properties of integration
Areas under curves
Finding areas under the curve involves definite integration. This means that whatever equation or graph that is integrated has a lower and an upper limit. There are a few things that should be cautioned for:
- Graphs intersecting x-axis
- Graphs that are not functions ("broken graphs)
- Areas between curves
Graphs intersecting x-axis
If a definite integral function contains a intersection between the x-axis and the graph,the final value would be whatever the area of the value on top of x-axis minus the area of the section under the x-axis. For example, graph of y=x(x+3)(x-4) is integrated between the lower limit of -4 and a upper limit of 0. The actual area of this graph would be bigger than the value worked out by solving the definite integral. There are multiple ways of avoiding this issue. The simplest of all is to divide the definite integral into parts to avoid having these intersections within the integral. So for the equation above, it would be divided into two definite integrals. The first would have be from -4 to -3 and the second would be from -3 to 0. It is important to remember that the integral with the graph under the x-axis would give a negative value. So take the absolute value that particular integral and add it to the remaining integrals to find the actual value.