Venn Diagram of Categorical Syllogisms

From WikiEducator
Jump to: navigation, search


SLMtitle.png Venn Diagram of Categorical Syllogisms



SLMtoc.png
Chapter Outline


• Meaning of venn diagram

• Basic strategies of using venn diagram

• Important Considering factors

• Arguments with conclusion in venn diagram

• Self assessment questions





SLMinto.png Introduction


One good method to test quickly syllogisms is the Venn diagram technique. This class assumes you are already familiar with diagramming categorical propositions. The technique of Venn diagrams for categorical syllogisms is based on the fact that in a valid syllogism, the conclusion asserts no more than what is already contained, implicitly, in the premises. If the conclusion asserts more than that, it does not follow from the premises, and the syllogism is invalid. The technique is to diagram the premises, and then see whether anything would have to be added in order to diagram what the conclusion asserts. If so, the syllogism is invalid; if not, it is valid. In this chapter we will discuss this widely used technique of testing syllogism.




SLMobj.png Learning Objectives
After reading this chapter, you are expected to learn about:


           Know what the venn diagram is;
           Identify the strategies of using venn diagram; and
           Show the diagram with arguments and conclusion.






"Meaning and Use of Venn diagram

It is often helpful to think of a term in a proposition as a circle containing the members of the relevant class. This is the method of Venn Diagrams, invented by the English mathematician John Venn. Venn diagram is a technique which is used to test syllogisms quickly. In other words it can be used to show literally the way in which the conclusion of a valid categorical syllogism is contained in the premises.


Basic Strategy

Here’s the overall strategy in using Venn diagrams: 

   –Make a diagram of the major and minor premises
     –See if the conclusion is already contained in the Venn        diagram   of the premises
           •If it is, the argument is valid
           •If it is not, the argument in invalid.

Important Considering Factors

Before doing your Venn diagram, it is important to know what you are looking for. There are four possible cases: 

             A proposition conclusion

             E proposition conclusion

             I proposition conclusion

             O proposition conclusion


Let’s consider each possibility.

Arguments with an A Conclusion • If the conclusion of a valid standard form categorical syllogism is an A proposition, the following area outlined in red in your Venn diagram must be shaded:

px 35


• Note that other areas may be shaded as well, but the minimum is that the area in red be completely shaded..

Arguments with an E Conclusion o If the conclusion of a valid standard form categorical syllogism is an E proposition, the following area outlined in red in your Venn diagram must be shaded: o


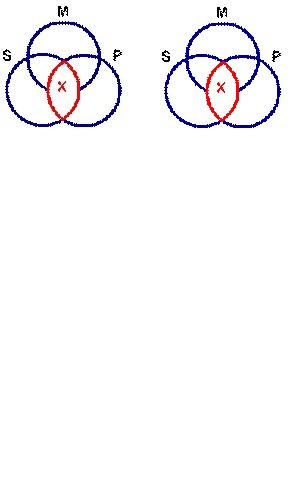
o Note that other areas may be shaded as well, but the minimum is that the area in red be completely shaded.. Arguments with an I Conclusion o If the conclusion of a valid standard form categorical syllogism is an I proposition, there must be an “x” somewhere the area outlined in red:


o Note that you just need an “x” anywhere in the area outlined in red, not in both regions. Arguments with an O Conclusion o If the conclusion of a valid standard form categorical syllogism is an O proposition, there must be an “x” somewhere the area outlined in red:


o Note that you just need an “x” anywhere in the area outlined in red, not in both regions. Example #1: AAA-1 

   Let’s begin with an AAA-1:

All M is P

All S is M

All S is P

Example #1: AAA-1 o First, diagram the major premise:

All M is P

All S is M

All S is P



Example #1: AAA-1

All M is P

All S is M

All S is P


Example #1: AAA-1

o Now let’s put both of them together on the same diagram:

All M is P

All S is M

All S is P


o Recall what we were looking for. We have it, so it’s valid.



Example #2: AAA-2 o Let’s begin with an AAA-1:

All P is M

All S is M

All S is P



Example #2: AAA-2 o First, diagram the major premise:

All P is M

All S is M

All S is P


Example #2: AAA-2 o Now let’s diagram the minor premise:

All P is M

All S is M

All S is P


Example #2: AAA-2 o Now let’s put both of them together on the same diagram:

All M is P

All S is M

All S is P


o Recall what we were looking for. We do not have it, so it’s invalid.




Example #3: EIO-1 Begin with an EIO-1:

No M is P

Some S is M

Some S is not P


Example #3: EIO-1 o First, diagram the major premise:

No M is P

Some S is M

Some S is not P


Example #3: EIO-1 Now let’s diagram the minor premise: No M is P

Some S is M

Some S is not P


o Notice that the “x” could go in either part of the area that S and M share. Example #3: EIO-1

o Now let’s put both of them together on the same diagram. Notice that the shading knocks the “x” off the line:

No M is P

Some S is M

Some S is not P


o Recall what we were looking for. We have it, so it’s valid.



Example #4: AIO-1

Begin with an EIO-1:

All M is P

Some S is M

Some S is not P


Example #4: AIO-1 o First, diagram the major premise:

All M is P

Some S is M

Some S is not P


Example #4: AIO-1 o Now let’s diagram the minor premise:

All M is P

Some S is M

Some S is not P

o Notice that the “x” could go in either part of the area that S and M share. Example #4: AIO-1 o Now let’s put both of them together on the same diagram. Notice that the shading knocks the “x” off the line:

All M is P

Some S is M

Some S is not P


o Recall what we were looking for. We don’t, so it’s invalid.




}}", using "

SLMsections.png
 {{{Section}}}

", "

Subsection.png
 {{{Subsection}}}

" as per your Chapter outline. To give "HEADING" to your section or sub-section, type-in

SLMsections.png
 HEADING
or
Subsection.png
 SUB-HEADING


After closing the curly brackets, from next line you can type-in the text.

You may use as many Self-Assessment Questions (SAQs) and other pedagogical features, e.g., SAQs, Notes, Important, etc., listed at the TEMPLATE page of BOU Project. -->

{{


}}



Subsection.png
 {{{Subsection}}}





SLMsum.png Results



SLMkp.png Key Points

The key points of this chapter are as follows:






SLMgloss1.png Glossary






{{SLMtest |||||||

Comprehension Questions

1. The technique of Venn diagrams is based on the fact that in a valid syllogism the conclusion 

a) asserts no more than what is already contained, implicitly, in the premises 	
b) asserts more than what is contained in the premises


2. For a syllogism to be valid, the combined diagram must 

a) contain all information asserted by the conclusion 	
b) either fail to shade out an area excluded by the conclusion, or fail to put an x where the conclusion requires one.

3. For a syllogism to be invalid, the combined diagram must

a) contain all information asserted by the conclusion b) either fail to shade out an area excluded by the conclusion, or fail to put an x where the conclusion requires one.

4. Which of the choices represent the Venn diagrams of the given categorical syllogism? 

      All of Shakespeare's dramas are in blank verse

      Some great plays are in blank verse 

      Some great plays are Shakespeare's dramas

a) b)


c) d)

5. According to the Venn diagrams, the previous syllogism is valid or invalid?

a)valid b)invalid

6. Which of the choices represent the Venn diagrams of the given categorical syllogism? 

           All vertebrates reproduce sexually

           All vertebrates are animals 

           All animals reproduce sexually			

        a)     b)
        c)     d)

7. According to the Venn diagrams the previous syllogism is valid or invalid?

a)valid b)invalid

8. Which of the choices represent the Venn diagrams of the given categorical syllogism? 

                        No A is B

                        Some A are not C 

                        Some C are not B

a) b) 

        c)    d)

9. According to the Venn diagrams the previous syllogism is valid or invalid? a)valid

b)invalid

10. Which of the choices represent the Venn diagrams of the given categorical syllogism? 

                No horned animals are carnivores

                All moose are horned animals 

                No moose are carnivores			

         a)    b)
         c)    d)


11. According to the Venn diagrams the previous syllogism is valid or invalid? a)valid b)invalid


SLMfeedb.png Answers to SAQs






SLMref.png References and Further Readings







Retrieved from "https://wikieducator.org/index.php?title=Venn_Diagram_of_Categorical_Syllogisms&oldid=135664"