User:Zlodziejka

i am a student at giselagymnasium

Block quote

=Sandbox=

x(t) = x₀+vt

[math]\Delta x[/math] = v [math]\Delta t[/math]

v = [math]\frac {x}{t}[/math]

v = [math]\frac{x_1 - x_0}{\Delta t}[/math]

x₁ (t) = x₂ (t)

x₁ + v₁t = x₂ + v₂t

x₁ - x₂ = (v₂ - v₁) * t

t = [math]\frac{x_1 - x_2}{v_2 - v_1}[/math]

= [math]\frac{173m - 25m}{28\ltmath\gt\frac{km}{h}[/math]}</math>

a) ges: Fahrzeuggeschwindigkeit
[math]\Delta x[/math] = 0 - 168 m = - 168m
[math]\Delta t[/math] = 12,5 sekunden

[math]\frac{\Delta x}{\Delta t}[/math] = v
v = - 13,44m/s = -48,3km/h b) t = 2 min 53 sek

168m + ( -13,4m/s ) 173s

= - 2,16km

Schön, dass Sie an der Lösung dieser Aufgabe gearbeitet haben!--White Eagle 12:11, 22 October 2007 (CEST)

c) t =

400px

übersetzung:

it follows in this case:

a= [math]\frac{v}{t}[/math]

(movement with constant aceleration from that rests)

if the venture owns already at the beginning of the movement a beginning speed [math]v_0[/math] so the functional equation is

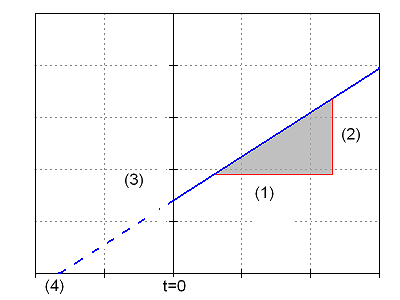
v(t) = [math]v_0[/math] + at

the graph is origin-straight a postponed:

(1) [math]\Delta t[/math]

(2) [math]\Delta v[/math]

(3) [math]v_0[/math]

(4) [math]t_0[/math]

It turns out for a>0 a movement with consistently acceleration, for a<0 a movement with consistently speed and for a=0 a movement with consistently delay ( falling graph)

!Attention! This time the formula a = [math]\frac{v}{t}[/math] is wrong!!

To be used is:

a is also the gradient of the line.

Definition:The acceleration a is the gradient of the t-v-line.

The unit of the acceleration is m/s².

2.3: Accelerationtest

Time it in s	Speed v in m/s
0	0
5	1

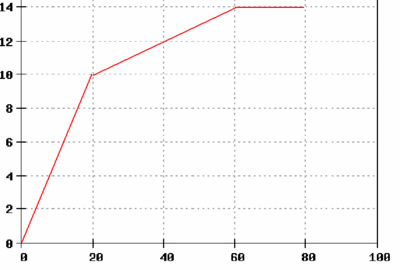
A testinstitution analyses the movement of a vehicle.The results are:

a) Draw a t-v-diagramm! (10s=1 cm, 1m/s=1 cm)

b) Name the type of movement in the particular timezones!

c) Find out the accelerations by using the graph!

5.7 a) geg: r = 1,0 m ges : v

F(gewicht) = F(zentral)

m w² r = m g /:m

w ² = r g

w ² = g : r

w ² = 9,81 N/Kg : 1,0m

w = [math]9,81[/math]

w = 3,13

v = w r

v = 3,13 * 1m

v = 3,13 m/s

b)

Rotor auf dem oktoberfest, mit Durchmesser d ,Boden wird abgesenkt ohne dass Körper (m= ...)abgleitet Welche Geschwindigkeit(wand)??