CONSUMER'S EQUILIBRIUM

MICROECONOMICS

CONSUMER'S EQUILIBRIUM

Introduction

All consumers strive to maximize their utility. We try to get as much satisfaction as we can. The consumer’s scale of preference is derived by means of indifference mapping that is a set of indifference curves which ranks the preferences of the consumer. Getting to the indifference curve which is farthest from the origin gives the highest total utility. Although the goal of the consumer is maximization of satisfaction, the means of achieving the goal is not clear. Higher indifference curve not only gives higher satisfaction but also are more expensive. Here we are confronted with the basic conflict between preferences and the prices of the commodities consumer wants to consume. With a given amount of money income to spent, we cannot attain the highest satisfaction but have to settle for less.

Learning Objectives

After reading this chapter, you are expected to learn about:

1.The consumer is to reach the highest indifference curve that is compatible with his budget constraint.
2.The consumer attains equilibrium when he is able to consume the most preferred commodity bundle which gives him the highest utility.
3. It is a state of stability where there is no tendency to rearrange the combinations of goods preferred by the consumer.

Assumptions

.

1.There are two goods i.e commodity X and commodity Y .
2.The consumer’s preference scale for combination of two goods is exhibited by indifference map.
3.The prices of goods are given and remain constant.
4.The consumer has a given income which sets to limits to his maximizing behavior.

Conditions for consumer's equilibrium

1.A given budget line must be tangent to an indifference curve , or the marginal rate of substitution between commodity X and commodity Y (MRS_x,y) must be equal to the price ratio between the two goods [math]\frac{PX}{PY}[/math].

2.At the point of equilibrium, indifference curve must be convex to the origin.

The limitation on utility maximization is evident. We want to reach the highest indifference curve with our limited income. You can go only as far as your budget constraint allows. Suppose you have only 50 rupees to spend on good X and good Y. The price of a unit of X is 10 rupees where as the price of good Y is 5 rupees. You can have as many as 5 units of good X if you want to forsake good Y. Similarly you can have 10 units of good Y with the same 50 rupees.The budget constraints illustrates all combination of goods you can buy with a limited income. In this case the budget line illustrates the combination of X and Y , that can be purchased with 50 rupees.

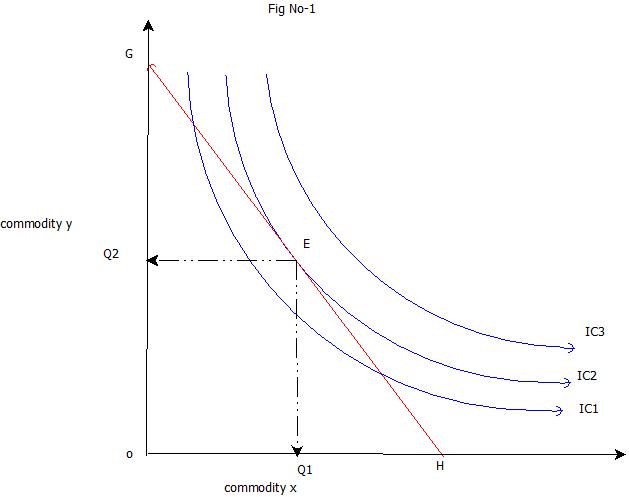
Above diagram explain the process of consumer’s equilibrium . The consumer’s preference scale is described by means of indifference mapping .Then we impose a budget line that reflects our income. In this case we have r 50 and the price of good X and good Y is r 10 and r 5 respectively. Therefore, we can afford only those combinations that are on or inside the price line GH.

In this diagram every combination on the price line GH cost you the same amount of money. In order to maximize the utility , we will try to reach the highest indifference curve which you could get with a given expenditure of money and given prices of two goods.The budget line touches IC2 at point E represents the most utility. This is the highest attainable indifference curve with which you can get OQ1 units of good X and OQ2 units of good Y for r 50. Any other affordable combinations on the price line GH gives you less satisfaction, because that will be on a lower indifference curve IC1. With this we conclude that the point of tangency between the budget line and an indifference curve represents optimal consumption. It is the affordable combination that maximize our utility.

At the tangency point E the slope of the price line GH and indifference curve are equal. Slope of the indifference curve shows the marginal rate of substitution of X for Y. The price line indicates the ratio between the prices of two goods (PX/PY). Thus at the equilibrium point E,MRSXY=Price of good x/Price of good y= PX/PY

The tangency between the given price line and an indifference curve is a necessary but not a sufficient condition consumer’s equilibrium .The second condition for consumer’s equilibrium is convexity of indifference curve to the origin .Which means MRSxy is falling at the point of equilibrium.

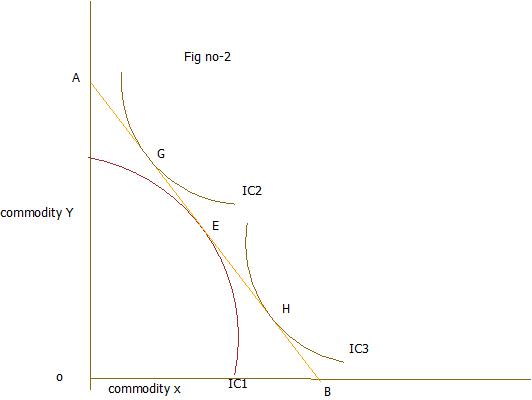
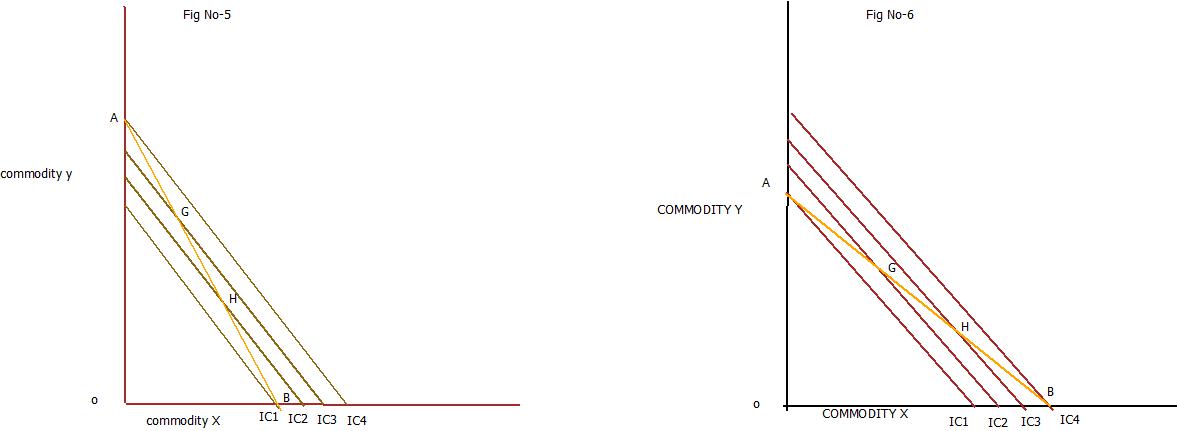
In fig no -1 indifference curve IC2 is convex to the origin at point E, is the optimum or best choice for the consumer .The consumer attains a stable equilibrium position where he is able to consume the most preferred combination which gives him highest utility. In figure no -2 ,IC1 is concave to the origin at point E. Price line AB is tangent to the indifference curve IC1 at point E and the marginal rate of substitution of X for Y is equal to the price ratio of two goods (PX/PY). But E cannot be the position of stable equilibrium because satisfaction would not be maximum .There are other combinations like G and H in the given price line will be on higher indifference curve .The congumer by moving along the given price line AB can go to other tangency pointsuch as G and H and obtain greater satisfaction than at point E.

Marginal Utility and Price

The slope of the indifference curve shows the marginal rate of substitution of good X for good Y, while the slope of price line indicates the ratio between prices of two goods i.e. ( PX /PY). Consaumer equilibrium was represented as the combination of good X and good Y can be written as

[math]\frac{MU of Good X}{Price of Good X}[/math] = [math]\frac{MU of Good Y}{Price of Good Y}[/math]

Alternatively,

[math]\frac{MU of Good X}{MU of Good Y }[/math] = [math]\frac{Price of Good X}{Price of Good Y}[/math]

This equation explains that at the point of equilibrium the relative marginal utilities of good X and good Y should equal to their relative prices. In other words , if good X cost twice as much as good Y , then marginal utility of good X must yield double , then the consumer is in an optimal state.

The slope of the budget constraint equal the relative prices of the two goods. In Fig-1, the slope of the price line equal to the price of goods X and good Y. It means the rate of substitution between the good X and good Y is 1:2. The relative marginal utilities of the two goods are reflected in the slope of the indifference curve. It is the marginal r ate of substitution which is equal to the relative marginal utilities of the two goods.

At the point of optimal consumption E in fig-1 the budget constraint is tangent to the indifference curve IC2. Which means,

[math]\frac{MU of Good X}{MU of Good Y }[/math] = [math]\frac{Price of Good X}{Price of Good Y}[/math]

Or Marginal rate of substitution of X for Y = [math]\frac{PX}{PY}[/math]

Consumer's Equilibrium and Non-normal cases

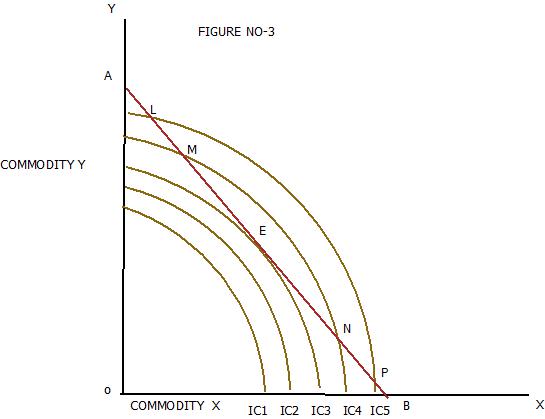
As we discussed earlier , indifference curves are usually convex to the origin .Convexity of indifference curve implies the marginal rate of substitution of X for Y decreases .The possibility of concavity cannot be ruled out in some exceptional cases. But at the same time concavity implies increasing marginal rate of substitution of X for Y .The consumer will choose or buy only one good.

Fig No-3

The price line AB is tangent to the indifference curve IC2 . But the consumer cannot be in equilibrium at point E because it can obtain grater satisfaction by moving along the given price line .Consumers satisfaction increases by either moving upward or downward till he reaches the extremity points A on the y-axis or B on the x –axis.

In these cases consumer will choose only one of two goods, depending on his scale of preference and level of satisfaction between good x and good y. In the above diagram A lies on a higher indifference curve than Therefore the consumer will choose only Y and buy OA of commodity Y. It is also noted that consumer is not tangent to the indifference curve at point A .Therefore consumer’s equilibrium cannot be establish at point A .

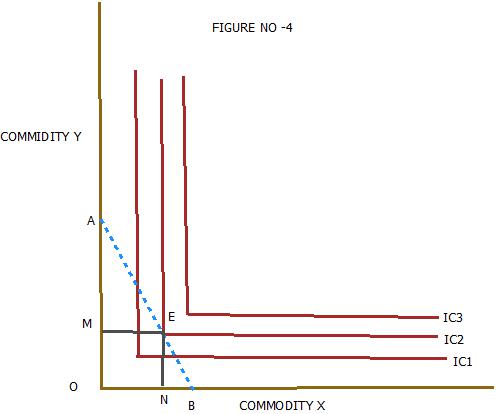
In case of perfect complementary goods ,the shape of the indifference curve have a right –angled .The equilibrium of the consumer cannot be established because only one point of the indifference curve is tangent to the price line AB.

Fig No-4

In figure no -4 the price line AB is tangent to the indifference curve at point E and no other tangency point is possible .There is no marginal rate of substitution between X and Y but only one combination is available with the consumer that is ON of X and OM of Y .

Activity

Study the following diagrams and establish consumer's equilibrium.

Fig No-5 and Fig No -6

	Self-Assessment Questions (SAQs) {{{n}}}
{{{SAQ}}}

1.Discuss the conditions of consumer's equilibrium.

2.Show with diagrame, how does a consumer maximize his satisfaction with limited income and given prices of two goods X & Y.

3.Why the marginal rate of substitution of X for Y decreases at the point of equilibrium?

4."The tangency between the given price line and an indifference curve is a necessary but not a sufficient condition consumer’s equilibrium ."Draw a diagrams to illustrate this statement.

Results

1. Indifference curves are usually convex to the origin .Convexity of indifference curve implies the marginal rate of substitution of X for Y decreases .

2.Consumer is confronted with the basic conflict between preferences and the prices of the commodities consumer wants to consume. With a given amount of money income to spent, we cannot attain the highest satisfaction but have to settle for less.

3.The slope of the indifference curve shows the marginal rate of substitution of good X for good Y, while the slope of price line indicates the ratio between prices of two goods i.e. ( PX /PY). Consaumer equilibrium was represented as the combination of good X and good Y can be written as :

[math]\frac{MU of Good X}{MU of Good Y }[/math] = [math]\frac{Price of Good X}{Price of Good Y}[/math]

Key Terms

Marginal rate of substitution-The rate at which one good is exchange for other.

Indifference map- A set of indifference curves which ranks the preferences of the consumer. Getting to the indifference curve which is farthest from the origin gives the highest total utility.

Price line-The slope of price line indicates the ratio between prices of two goods i.e. ( PX /PY).

Budget constraint-The budget constraints illustrates all combination of goods you can buy with a limited income. In this case the budget line illustrates the combination of X and Y , that can be purchased with limited resources.

Convexity of the indifference curve-Convexity of indifference curve implies the marginal rate of substitution of X for Y decreases .The possibility of concavity cannot be ruled out in some exceptional cases.

CONSUMER'S EQUILIBRIUM

MICROECONOMICS

MICROECONOMICS

Multichoice Questions

Navigation menu

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Print/export

Tools