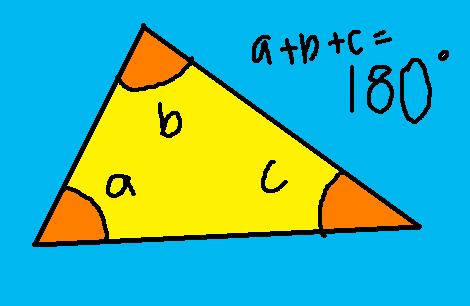User:Pallan/NCEAMath1.9

Work in progress, expect frequent changes. Help and feedback is welcome. See discussion page.

NCEA Level One Mathematics 1.9 Geometrial Reasoning AS90153

New Zealand Student sit NCEA in years 11,12 and 13 of schooling. Studyit is a very helpful website for students. This is a work in progress.

Rules to learn

Intersection Rules

These rules are in relation to a point of intersection. Rays or lines can intersect at a point. Rays start at a point and go on for ever, lines go on forever in both directions.

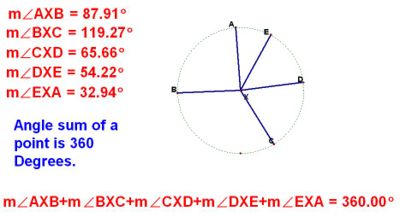
Angles at a point add to 360 degrees

There can be 2 or more angles at a point. It does not matter how many angles there are or the size of the angles. The important thing is that they will always add to 360 degrees.
The example shown has 5 angles which add to 360 degrees.

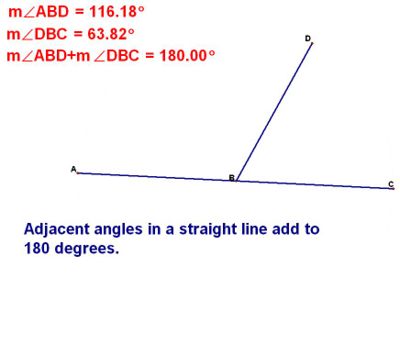
Adjacent angles in a straight line add to 180 degrees

A straight line is 180 degrees, half a turn, or half of 360 degrees. When a ray starts at a point on a line the adjacent (side by side) angles will always add to 180 degrees.

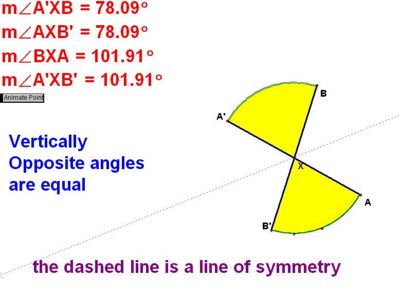
Vertically Opposite angles are equal

The proof for this is simple. Think about the straight line rule. The Vertically Opposite rule has 4 sets of "angles on a straight line" so the yellow angles must be equal. Also the dashed line show the line of symmetry.

Triangles

A 3 sided polygon is called a triangle.

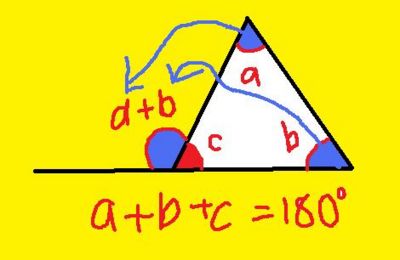
Angle sum of a triangle is 180 degrees

• 

  Angles in a Triangle add to 180 degrees

• 

  All Triangles Tesselate

• 

  Angles in a Straight line add to 180 degrees

The proof is that any triangle tesselates. You can make your own triangle and tear it into 3 pieces, the 3 pieces will lie in a straight line.

Exterior angle of a triangle equals sum of the two opposite internal angles

Base Angles in an isosceles triangle are equal

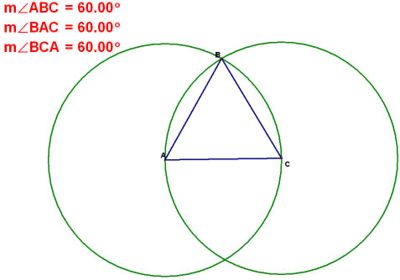
Angle in an equilateral triangle are 60 degrees

The visual proof works like this: The two circles share the same radius, therefore the 3 sides of the triangle drawn are the same length. Because the resulting shape has 3 equal angles because of the symetry, the angles must be 60 degrees because angles is a triangle add up to 180 degrees.

Polygons

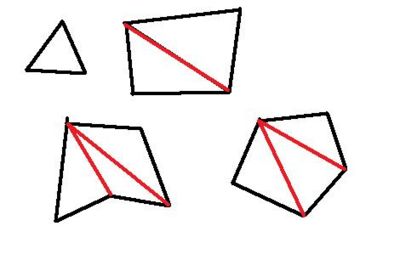
Internal angles of an n sided polygon add to 180*(n-2)

Take the number of sides of a polygon less two, this gives the number of triangles worth of angles in the polygon. So mutiply by 180 degrees, because there are 180 degrees in a triangle. 3 sided polygon is a triangle and the internal angles add to 180 degrees. 4 sided polygon is a quadrilateril and the internal angles add to 360 degrees. 5 sided polygon is a pentagon and the internal angles add to 540 degrees. 6 sided polygon is a hexagon and the internal angles add to 720 degrees.

External angles of polygon add to 360 degrees

No matter how many sides a polygon has the exterior angles add to 360 degrees because you must end up where you started, turning a full circle.

Internal angles of a regular n sided polygon are 180*(n-2)/n degrees

A regular polygon has all angles the same size and all sides the same length. Because all the angles are the same and we know what the internal angles add up to from the rule above, we simply take the total and divide by the number of angles. (The number of angles is equal to the number of sides).

External angles of a regular n sided polygon are 360/n degrees

We know the external angles of any polygon add to 360, and an n sides polygon has n external sides. Because in a regular polygon all the angles are equal we can calculate their size by dividing 360 by n.

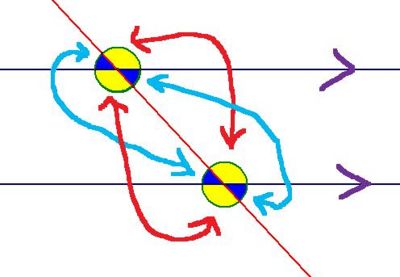
Parallel Lines

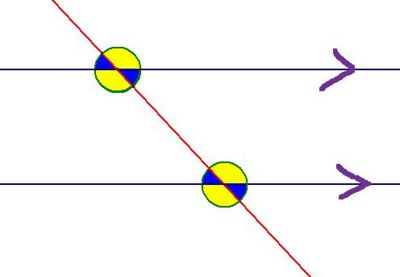
The transversal is the red line, the other two lines are parellal to each other which is indicated by the arrows. The 'big idea' here is that all the yellow angles are equal and all the blue angles are equal.

Corresponding angles on parallel lines are equal

The arrows are pointing out the four pairs of corresponding angles.

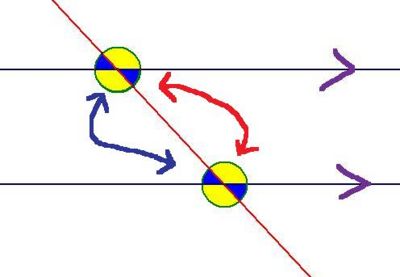
Cointerior angles on parallel lines add to 180 degrees

The arrows are pointing out the two pairs of cointerior angles.

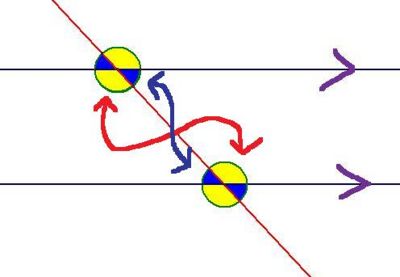
Alternate angles on parallel lines are equal

The arrows are pointing out the two pairs of alternate angles.

Circles

These rules are all extensions of the isosceles triangle "base angles are equal" rule, angles on a straight line and angles at a point. If you spend time understanding the connections between the above rules and how they prove the rules below it will be easier to remember all the rules for assesment.

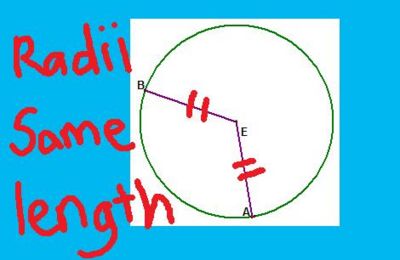
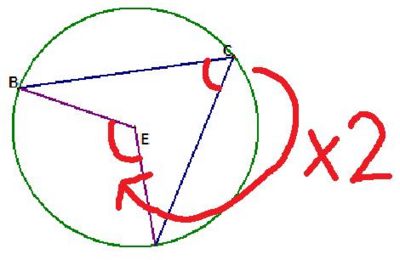
Angles at the centre is twice the angle at the circumference

The proof of this is to create two isosceles triangles.

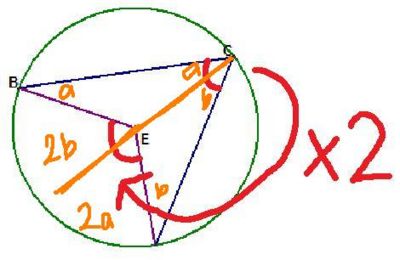
Angles from the same arc are equal

This is automaticly true if "Angles at the centre is twice the angle at the circumference" is true.

To prove this concider the angle at the centre rule.

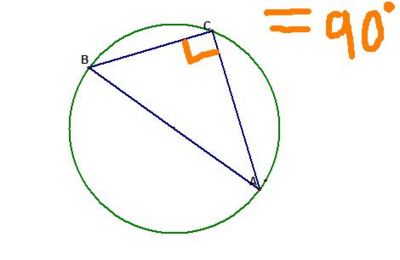
Angles in a semicircle are 90 degrees

This rule is the special case of "Angles at the centre is twice the angle at the circumference" where the angle at the centre is 180, and the angle at the circumference is 90 degrees.

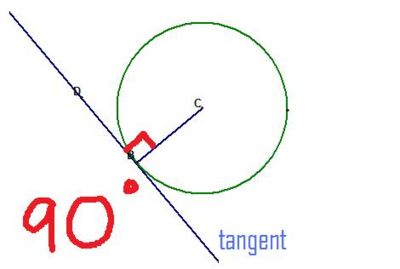
The angle between a tangent and a radius is 90 degrees

As a tangent is a line that touches the circle at only one point, it must touch at right angles to the radius at that point.

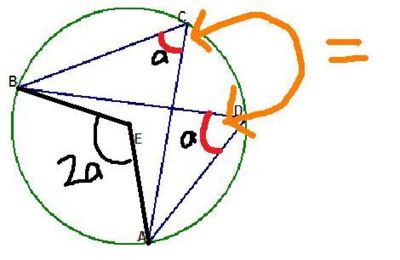
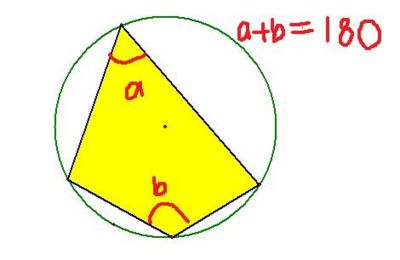
Opposite angles in a cyclic quadrilateral add to 180 degrees

This is an extension of "Angles at the centre is twice the angle at the circumference", looking at the two different arcs from the same points. The angles at the centre add to 360 degrees, so the angles at the circumference add to half 360 which is 180 degrees.

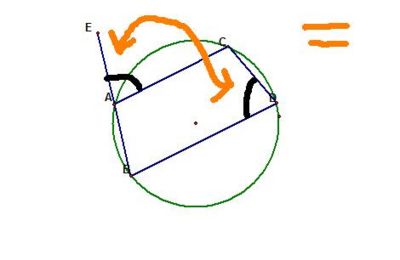
The exterior angle of a cyclic quadrilateral equals the opposite interior angle

This extends from "Opposite angles in a cyclic quadrilateral add to 180 degrees" and "Adjacent angles in a straight line add to 180".

Symmetry

If there is a line of symmetry then the angles that are reflected in the line will be the same.

Strategies

Strategies for finding angles using Geometrical Reasoning.

Label the obvious ones first.

Extend line segments to see the connections a different way.

Draw an extra parallel line if you think it may help.

Turn the book around to see the problem from another angle.

External Resources

GeoSketchPad File BBC Angle Facts BBC more facts BBC Polygons BBC Circles BBC Circles 2 BBC Parallel Lines BBC Polygons BBC Similar Shapes