User:Max

Hello

My name is max and i'm joining the education project of White Eagle for the 11th grade on Gisela Gymnasium] (secondary school).

Aufgabe 1.0 :

Alles ist in Bewegung, da die Körper auf denen wir uns befinden sich letztlich auch bewgen(Erdrotation, Bewgung der Sonne in unserer Galaxie usw.).

Nichts ist in Bewegung, wenn man sich z.B auf einem von zwei sich prarallel bewegenden Planten befindet und zum Anderen hínüberblickt, scheint es als ob sich dieser in Ruhe befinden würde.

Aufgabe1.1

e) A)1,8 t*km/h bei 50 HZ

   B)2,7 t*km/h

a) Die Bewegung verläuft nach der Beschleunigungsphase konstant b) 100 Hz -> 200 tupfen/S Abstand 2 Tupfen 0,005 s c) das Wägelchen ist in Fall B schneller d) eine schiefe Ebene

Sandbox

Helo! Helo!

[math]x(t)= v_0+ v*t [/math]

[math]\Delta x = v*\Delta t[/math]

[math]v= \frac {x}{t}[/math]

[math]v = \frac{x_1-x_0}{\Delta t}[/math]

[math]x_1(t) = x_2(t)[/math]

[math]x_1+v_1*t = x_2+v_2*t[/math]

[math]x_1-x_2 = (v_2-v_1)*t[/math]

[math]t=\frac{x_1-x_2}{v_2-v_1}[/math]

[math] = \frac{173km-25km}{28\frac{km}{h}-11\frac{km}{h}}[/math]

--Max 11:56, 5 October 2007 (CEST)

Graphen

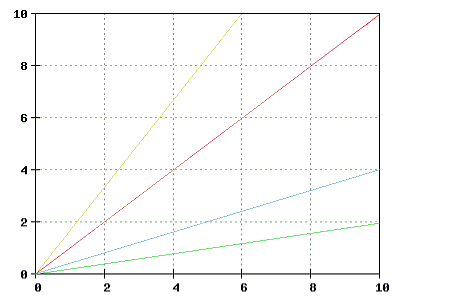--Max 12:05, 9 November 2007 (CET)

Aufgabe 2.1

Die Abstände zwischen den Punkten werden im Laufe der Zeit größer.

Aufgabe 2.2

Punkte	Abstand	Geschwindigkeit
1-2	0,45mm	22,5[math]\frac{mm}{s}[/math]
2-3	1mm	50[math]\frac{mm}{s}[/math]
3-4	2mm	100[math]\frac{mm}{s}[/math]
4-5	2,22mm	111[math]\frac{mm}{s}[/math]
5-6	2,7mm	135[math]\frac{mm}{s}[/math]
6-7	3,4mm	170[math]\frac{mm}{s}[/math]
7-8	3,6mm	180[math]\frac{mm}{s}[/math]
8-9	4,3mm	215[math]\frac{mm}{s}[/math]
9-10	4,8mm	240[math]\frac{mm}{s}[/math]
15-16	7,5mm	375[math]\frac{mm}{s}[/math]
20-21	10mm	500[math]\frac{mm}{s}[/math]
25-26	12,9mm	645[math]\frac{mm}{s}[/math]
30-31	15mm	750[math]\frac{mm}{s}[/math]
33-34	16mm	800[math]\frac{mm}{s}[/math]

Die Beschleunigung ist bei Abb 2 kleiner, da die Abstände zwischen den Punkten langsamer wachsen.

Lösung zur Extemporalen Gruppe A

a) Graph :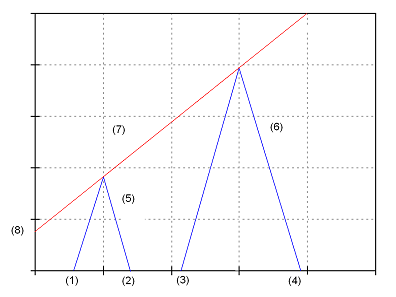 x-Achse t Zeit, y-Achse x Ort

b)

  geg : [math]t_1 = 0,65s  t_2 = 0,95s[/math]

  geg : [math]t_3 = 3,80s  t_4 = 4;80s [/math]
  
  geg: [math]v_s =340\frac{m}{s}[/math]

[math]\Delta t = t_2-t_1 [/math]

[math]0,95s-0,65s = 0,30s[/math]

[math]x_1 = v_s*\frac{\Delta t}{s}[/math]

[math]340\frac{m}{s}* 0,15s[/math]

[math]= 51m[/math]

[math]x_2 = 170m[/math]

[math]\Delta x = 170m -51m = 119m[/math]

[math]\Delta t = 4,30s-0,80s = 3,50s[/math]

[math]\frac{\Delta x}{\Delta t} = v[/math]

[math]\frac{119m}{3,5s} = 34\frac{m}{s} = 122\frac{km}{h}[/math]

c)

[math]x= x_0+ v*t[/math]

[math]X_0 = x-v*t[/math]

[math]x_0 = 51m- 34\frac{m}{s}*0,8s[/math]

[math]= 24m[/math]

--Max 12:22, 19 October 2007 (CEST)

Schön, dass Sie an der Lösung dieser Aufgabe gearbeitet haben!

Verwenden Sie Zwischenüberschriften!--White Eagle 12:16, 22 October 2007 (CEST)