User:Kbhole/New project

New Project

Theory of Measurements

Contents

1. Introduction
2. Possible error and precision
3. Accuracy and absolute and relative errors
4. Significant digits
5. Dropping of a nonsignificant digits
6. Rounding of numbers
7. Rounding error
8. Absolute and relative errors

<fck:hr>

1. Introduction

To quantify physical quantities, scientists use various devices and thereby quantify physical quantities. However, no physical measurement is ever exact. The accuracy of measurement is limited by the degree of refinement of the instrument and by the skill of the observer.But even with highly skilled observer using most refined instrument, the measurement made will not be exact in absolute sense. This is due to the fact that every observation in a measurement is the outcome of human judgement and it can never be a subject of mathematical exactness. Normally we express these measurements as approximate numbers. We distinguish two measurements 3.2 cm and 3.20 cm. These are the results of measurements using different devices. Secondly, while doing computations with such numbers special care is required. The ratio 32.1 / 12 is expressed as 2.7 and not as 2.68 or 2.675. The number of digits used in measurement have some significance regarding the quality of the measuring instruments.

2. Possible error and precision

Many of the measuring instruments have zero error which may cause inexact measurement. Secondly, error can also be caused due to limitations of human judgement and perception.

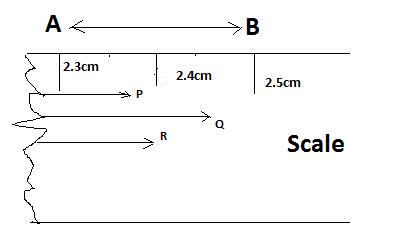
Let us consider a perfect  centimeter scale graduated with clear and equal makings of millimeters.If we need to measure the lengths of the arrows shown in figure. We will presume that the tails of the arrows are perfectly aligned with zero mark.The arrowhead of  P  arrow is closure to the 2.4 mark than 2.3 cm mark. The head of the Q arrow is closure to 2.4 mark than 2.5 mark. Hence its length will also be reported as 2.4 cm. Similarly the length of the arrow R would be reported as 2.4 cm. The Measurement reported as 2.4cm  may be errornous by 0.05 cm which is half of the unit of measure i.e., 0.1 cm. This means the measurements are reported with its last digit as uncertain. In 2.4 cm, the last digit 4 is uncertain. The last digit is always estimated but it cannot be ignored because it gives definite information about the measurement.   

This means, baring any mistake in  measurement, the maximum possible error is equal to the unit of measurement. The possible error is due to inherent imprecision in measuring devices. Measuring devices having less possible error are more precise. Hence measurement reported 2.43 cm is more precise than a measurement reported to the tenth of the centimeter such as 2.4. 

3. Accuracy and absolute and relative errors

In order to compare the accuracy of the measurement, we define the absolute error as the magnitude of the difference between the exact value and the approximation. The relative erroris defined as the ratio of the absolute error to the maginitude of the exact value.

Significant digits

The number of digits that carry some information about the measured value of a quantity are known as "significant figures". The values having more significant figures is more reliable than the one having less number of significant figures for the same measurement. For reliability of measurements, writing exact number of significant digits is the simplest way rather than writing more digits than what are relevant to a measurement.

Rules for determining significant digits

1. All non-zero digits are significant
2. Zeroes which occur between two nonzero digits are also significant.
3. Zeroes to the left of the left most nonzero digit are never significant.
4. Zeroes to the right of the right most nonzero digit are significant only if they come from the measurement.

The numbers 321, 3.02, 0.321 and 0.0321, all have three significant digits.

Table

Measurement	Unit of measurement	Possible error	Relative error
0.5 m	0.1 m	0.05 m	0.1
0.05	0.01	0.005	0.1
0.005 m	0.001 m	0.0005 m	0.1
0.0005	0.0001	0.00005	0.1

This shows that the unit of measure and the possible error in all the cases are different. But the relative error is the same. It indicates that these zeroes are not significant because they do not affect relative error. Hence one can conclude that a digit is significant if and only if it affects the relative error.

Dropping of a nonsignificant digits

The derived quantities like volume, specific heat,are to be computed using directly observed quantities.this computation requires arithmatic operations like addition, subtraction, multiplication and division. In order to avoid meaningless surplus digits in the computed answer, some conventions are to be followed. this also reduce the amount of computation.

1. Unless otherwise stated, it may be asssumed that the last digit in the statement of the measured quantity is uncertain by one unit.
2. If it is desired to express certain quantity in multiples and submultiples of its units, zeroes should not be used to show the location of the decimal point. The location should be indicated by using an appropriate power of 10. This also makes the multiplication and division of numbers convenient.

Rounding of numbers

Sometimes it necessary to round of a given number to one having less number of digits by disregarding the unwanted digits.The process of omitting the superfluous digits and retaining only the desired ones is called rounding.

Rounding error

If we round off the number of digits that are significant, the error caused in rounding is much larger than in the number itself. In computations, one deals with rounded numbers and hence rounding errors will determine the error in the computed result. If a number is correct upto 5.321, the error in it is 0.0005. Rounded to two digits, it will be 5.3. The rounding error is 5.321-5.3 = 0.321. This is much more than inherent error 0.0005.

Absolute error and Relative error

The relative error (e_r), which is also called the proportional error. The maximum relative error is always less than the ratio of maximum absolute arror to the difference between the actual reading and the maximum absolute error. For example, if the reading taken is 2.35, then the absolute error is
(e_a) <0.01 x 0.5 =0.005.

The relative error (e_r) <0.005/(2.35-0.005) = 0.0021
The relative error is a pure number and has no units.

Refrences

• John Robert Taylor:An Introduction to Error Analysis:

The Study of Uncertainties in Physical Measurements

• Yardley Beers: Introduction to the theory of error.