User:Chris1727

    =Sandbox=

Text

Kursiv

[math]x(t)=x_0 + vt[/math]

[math]\Delta x = v \Delta t[/math]

[math]v = \frac{x}{t}[/math]

[math]v = \frac{x_1 - x_0}{\Delta t}[/math]

[math]x_1(t) = x_2(t)[/math] </math> [math]x_1 + v_1 t = x_2 + v_2 t[/math]

[math]x_1 - x_2 = (v_2 - v_1) t[/math]

[math]t = \frac{x_1 - x_2}{v_2 - v_1} = \frac{173 m - 25 m}{28 km /h - 11 km/h}[/math]

= Aufgabe 1.10 =

b)

Schön, dass Sie an der Lösung dieser Aufgabe gearbeitet haben!--White Eagle 12:12, 22 October 2007 (CEST)

[math]x_1 = x_0 + v t[/math]

[math]x_1 = 47.7km + 45 \frac{m}{s} 4870s [/math]

[math]x_1 = 266.9km[/math]

Geschwindigkeit PKW

[math]v_2 = \frac{\Delta x }{\Delta t } = \frac{266.9km - 15.2km}{4800s} = 52.4 \frac{m}{s}[/math]

c)

aus b) folgt:

266.9km - 47.7km = 219.2km = Strecke des LKW

266.9km - 15.2km = 251.7km = Strecke des PKW

Übersetzung

It follows in this case:

[math]a =\frac{v}{t}[/math]

(Movement with constant acceleration from that rests)

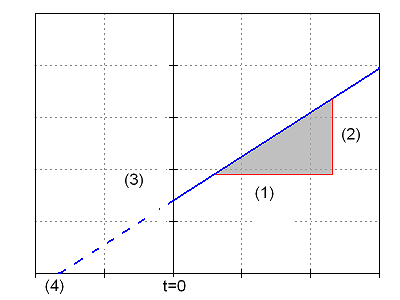
If the venture has already at the beginning of the movement a beginning speed [math]v_0[/math] so the functional equation is

[math]v(t) = v_0 + a t[/math]

The graph is a postponed origin-straight

[math](1)\Delta t[/math]

[math](2)\Delta v[/math]

[math](3)v_0[/math]

[math](4) t_0[/math]

It tourns out for a>0 a movement with acceleration,for a = 0 a movement with constant speed and for a<0 a movement with constant delay(falling graph)

!Attention! This time the formula[math] a = \frac{v}{t}[/math] is wrong!!

To be used is:

[math]a = \frac{\Delta v}{\Delta t}[/math]

a is also the gradient of the line

Definition: The accleretation a is the gradient of the t-v-graph

The unit of the acceleration is m/s²

Problem 2.3: Accelerationtest

A testinstitution analyses the movement of a vehicle.The results are:

Time t in s	Speed v in m/s
0	5	10	60	80	100	110	120	130
0	1	2	12	12	12	8	4	0

a) Draw a t-v-diagramm! (10s=1 cm, 1m/s=1 cm) 

b) Name the type of movement in the particular timezones! 

c) Find out the accelerations by using the graph!