UCTL/Physics/Context Rich Problems
.gif)
Welcome to the UCTL space on WikiEducator.
Strategies to Support Active Learning
Contents
Teaching Strategy 2: A New Type of Problem; Context Rich Problems
This term ‘context rich problem’ comes from work undertaken at the University of Minnesota, Department of Physics. It is used here in a specific sense, defined below. In many ways in this country there has been an intentional swing towards this type of problems over the past decade. There is however more to learn as shown in some of the work from Minnesota.
In summary:
Their research has shown that the use of context rich problems in cooperative learning groups can lead to dramatic improvement in the understanding of basic concepts. This section is adapted from material at their web site http://www.physics.umn.edu/groups/physed/projects.html
What are context Rich Problems
As defined by the University of Minnesota, these problems have several characteristics:
1. The problem need to be challenging enough so that a single student cannot solve it, but not so challenging that a group cannot solve it. 2. The problem should be structured so that the group can make decisions on how to proceed with the problem. 3. All the required information may not be given, for example the weight of a person or a distance that may be easily estimated. Furthermore, extra information may be given that is not required to solve the problem. 4. The problem should be relevant to the lives of the students. (!) 5. The problem should not depend on students knowing a trick nor should they be mathematically tedious.
In short traditional end-of-chapter textbook problems are inadequate. The context rich problems have been created to satisfy these constraints. They are strikingly different from traditional problems.
Context rich problems are designed to encourage students to use an organised and logical problem solving strategy instead of mere formula driven random search strategies. They are designed to force the students to consider concepts in the context of real objects in the real world and to see the problem solving activity as a process, a series of decisions which uses fundamental concepts to analyse a problem. This analysis should be qualitative before mathematical manipulation of formulas.
The Maryland problems have these characteristics:
- Each problem is a short story in which the major character is the student and they use the personal pronoun.
- It includes plausible motivation or reason for you to calculate something.
- The objects in the problems are real or can be imagined.
- Typically no pictures or diagrams are given. Students need to actively visualise the situation using their own experience.
- The problem cannot be solved in one step by plugging numbers into a formula.
Each characteristic emphasises the need for the student to make decisions using their physics knowledge. They discourage the view that problem solving in physics in purely a mathematical exercise of choosing the right problem then plugging in numbers which usually have no real-world application for an average person.
Further, more difficult context rich problems may include these features:
- The unknown variable may not be explicitly specified in the problem statement. For example, a question after a description of a situation the conclusion may be something like “Will the design work?” or “Do you believe the boy’s story?” These types of statement encourage students to practice reducing a problem to something they can calculate, but actively forces thinking as to what to calculate.
- Assumptions may need to be made to solve the problem. For example, they may need to assume a reasonable value for a person’s mass or they may need to assume an idealisation to make the problem solvable.
- A problem may require the use of more than one fundamental principal if it is to be solved. For example, Newton’s Laws and conservation of energy.
These characteristics reinforce the idea that problem solving is a decision making process. It emphasises the need for students to use their conceptual understanding of ideas to analyse the problem before introducing equations.
Some common contexts include:
1. Physical work. Pushing, pulling, lifting objects and so on. 2. Suspending objects, falling objects. 3. Sports situations. 4. Situations involving the motion of bicycles, cars, boats, trucks and planes. 5. Up in space. The motion of satellites and planets. 6. Heat and cooling, for example. Cooking, freezing and burning.
Experience has shown that students working in well structured collaborative groups can achieve more than the same students working on their own
Creating context rich problems
One way to invent a context rich problem is to start with a textbook exercise or problem and then modify it. Here are some possible steps:
1. Always start with the word “You”. This personalises and motivates the problem for the students.
2. If necessary determine a context and decide on a motivation. Why would anybody want to calculate something in this context? Optional – write the problem like a short story.
3. Decide on how many difficulty characteristics you want to include a) extra information b) leaving out common knowledge, for example the exoneration due to gravity c) writing the problem so that the target variable is not explicitly stated d) thinking of information so that two distinct approaches are needed for example forces and kinematics. 4. Check the problem to make sure it is solvable, the physics is straightforward and the mathematics is reasonable.
Sometimes it is difficult to think of a motivation. Here are some that have been used by the Maryland writers:
- You are (fishing, swimming, climbing, riding a bike) and you notice . . .
- You are watching TV or reading an article about …………. and wonder …………
- Because of your knowledge of physics you’re friend asks you to help him or her …………
- You are writing a short adventure story for your English class about ……… and need to figure out …………
- You are a consultant for (an engineering firm, a movie, a trucking business, a Martian survey mission) and you are asked to (evaluate, recommend, test) …. What do you say?
An Example of a Context Rich Problem.
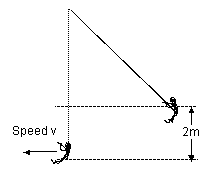
Note: a diagram is included here. Rules are made to be broken.
Example: ASSESSED PROBLEM SHEET 1.
Answer on sheet provided. Work together in a group handing in one combined solution.
Assign roles, but you choose how well you work with these.
Time: 20 minutes. Fill in the times taken.
Full access to notes, textbook is allowed.
|
The Catburglar’s grappling hook Joe the midnight catburglar comes to you for some advice. He has to develop a lightweight grappling hook and a cord from fine nylon strands, each strand of which can withstand a maximum tension of 4.5N. He requires a length of 5 m and will need to swing from heights of at most 2 m (above the lowest position of the rope) as shown. You do some calculations for him (against your better judgement of course) to recommend how many strands should make up the cord. You pause for a moment and realise you are short one vital piece of information. You make a sensible estimate and then work on a solution. This is the question: Assuming you are truthful, what do you tell him?  |
From the data the maximum tension is 1.8W where @ is the weight force of the cat burglar. The mass of the cat burglar is not specified. The answer asks for the specific number of strands - ie the maximum tension should be divided by 4.5N for a correct answer. An extra few strands should be allowed for safety.
