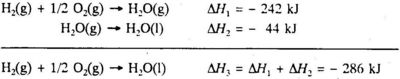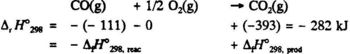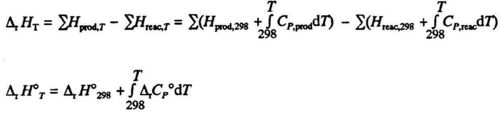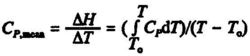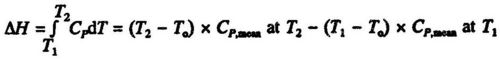The1stLawofThermodynamicsLesson5

THERMOCHEMISTRY

When a chemical reaction takes place, heat (positive or negative) is absorbed by the system. This heat can be determined• experimentally in a calorimeter at constant volume (q = Δ_rU), or at constant pressure(q = Δ_rU).

Enthalpy is a state function, and the enthalpy of reaction is independent of the reaction path. Thus we may choose any convenient path in order to calculate the enthalpy of reaction. There is no absolute value for the enthalpy of a system. In order to calculate and compare enthalpies of reaction (which have absolute values) standard states are introduced. Enthalpies of formation in the standard state are listed in tables.

The enthalpy change of a reaction is temperature dependent. The temperature dependence is determined by the change in heat capacity by the reaction.

An aqueous solution is always electrically neutral. In the solution of an electrolyte we always have both positive and negative ions. The enthalpy of formation of single ions listed in tables are based on the convention that the enthalpy of formation of H⁺(aq) is arbitrarily given the value zero. The conventional enthalpy of formation of a single ion is based on the standard that Δ_rH⁰(H⁺,aq) = O.

MEASUREMENT OF HEAT OF REACTION

When a chemical reaction takes place, there will be a change in the internal energy of the system. This change cannot be measuted directly, we can only measure the mechanical work performed on the surroundings and the heat received by the surroundings. If we arrange an experiment such that no work is carried out during the chemical reaction, we will have Δ_rU = q. in the field of organic chemistry combustion reactions are of great interest. An organic compound and an excess of oxygen are placed in a closed container immersed in a water bath (a bomb calorimeter). The teaction is ignited by heating electrically a small piece of resistance wire. The temperature inc:rcase of the water upon the reaction is measured, and with the knowledge of the heat capacity of the calorimeter, the amount of heat evolved (-q) can be calculated. The volume is constant and no work bas been carried out.

Thus we can find Δ_rU = U_prod - U_reac = q for the reaction. Since many chemical reactions take place at constant pressure (atmospheric pressure), we are also interested in measuring the heat evolved under these conditions, when pressure - volume work is the only work carried out. In this case we have Δ_rH = q If we let a chemical reaction take place in a calorimeter open to the atmosphere, pressure - volume work is allowed to take place. From the measured temperature change of the water in the calorimeter and the known heat capacity we calculate the heat evolved (-q). Under these conditions we have Δ_rH = H_prod - H_reac = q

Since ΔH = ΔU + Δ(PV), see eq. (3.10), we can calculate ΔH from ΔU and vice versa, when Δ(PV) is known. For an ideal gas we have ΔH = ΔU + Δ(nRT), see eq. (3.16). At constant temperature ΔH = ΔU + Δ(nRT), where Δ_n is the change in the amount of gas components by the reaction.

For reactions in which only liquids and solids are involved, very little volume change occurs. If the reactions take place at the relatively low pressure of 1 atm, the pressure - volume work is very small, and we have Δ_rH ≈ Δ_rU. For reactions in which both condensed phases and gases are involved, Δ_rH ≈ Δ_rU + Δ_nRT where Δ_nis the change in amounts of only the gas components. Direct measurement of heat of reaction can only be carried out for quantitative reactions (amounts of reactants left after reaction, and products formed by side reactions are insignificantly small). The procedure for measuring heats of reaction may be found in textbooks of experimentical physical chemistry.

THERMOCHEMICAL EQUATIONS

The heat energy involved in a neutralisation reaction may be measured in a calorimeter at atmospheric pressure, and this information may be combined with the chemical equation for the reaction to give a thermochemical equation. For the neutralization of a strong acid by a strong base in aqueous solution we have:

HCL(aq) + NaOH(aq) → NaCl(aq) + H₂O Δ_rH = -56 kJ (5.1)

The negative sign for the enthalpy shows that the system loses energy as it undergoes the change, energy is released, i.e., the reaction is exothermic. For an endotermic reaction the enthalpy of reaction has a positive sign. Since the essential step in the neutralization reaction is the formation of water from the ions, we may write the net equation:

H⁺ + OH^- → H₂O Δ_rH = -56 kJ

The enthalpy of neutralizing a strong acid with a strong base is - 56 kJ mol^-1.

In a thermochemical equation the quantities of materials involved are molar amounts of reactants and reaction products as prescribed by the equation. Thus in eq. (4.1) one mole of HCL reacting with one mole of NaOH produces one mole of NaCl and one mole of H₂O with the enthalpy change - 56 kJ. The equation:

H₂O(g) + O₂(g) → H₂O(l) Δ_rH = -572 kJ

tells us that when two moles of hydrogen gas react with one mole of oxygen gas to form two moles of liquid water, the enthalpy change is - 572 kJ. The reaction is exothermic. The enthalpy change per mole liquid water formed is obtained by dividing the thermochemical equation by 2:

H2(g) + 1/2O2(g) →  H2O(l)                  ΔfH = -286 kJ(5.2)

The states of the substances must be specified in a thermochemical equation, because the enthalpy change depends on the state of the reactants and the products. The gaseous state is given by the suffix (g) after the chemical formula, the liquid state is given by the suffix (l) and the solid state is given by the suffix (s). A substance in aqueous solution is given the suffix (aq). If gaseous water is formed instead of liquid water, the enthalpy change per mole gaseous water formed is - 242 kJ:

H₂(g) + 1/2O₂(g) → H₂O(g) Δ_fH = -242 kJ(5.3)

ADDITIVITY OF ENTHALPY CHANGES

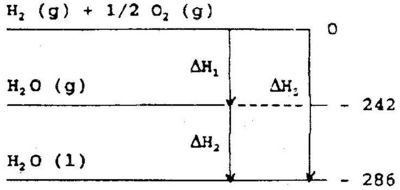
The enthalpy is a state function, thus the change in enthalpy, ΔH, depends on the final and initial state only, regardless of the pathway from the initial to the final state. This is illustrated in Fig 5.1

Fig5.1 The additivity of enthalpy change

We may produce one mole of liquid water from hydrogen gas and oxygen gas in two steps. In the first step water vapour is produced, and in the second step it is condensed to liquid water - or we may produce the liquid water directly. in both cases the total enthalpy change will be the same.

This principle of additivity is frequently called Hess' law of constant heat summation. Hess' law enables us to calculate enthalpy changes for reactions that are not easily carried out quantitatively in a calorimeter. The equation:

C(graph) + 0₂(g) → CO₂(g) ΔH₁ = - 394 kJ(5.4)

tells us that when one mole solid carbon in the form of graphite reacts with one mole oxygen gas to form one mole carbon dioxide gas. the enthalpy change is - 394 kJ. An amount of heat, + 394 kJ, is given off to the surroundings by the exothermic combustion reaction. The combustion of carbon to form carbon dioxide can be carried out quantitatively in a calorimeter. The same is true for the reaction:

CO(g) + 1/2 02(g) → CO2(g) ΔH2 = - 283 kJ 

In contrast the reaction of carbon to carbon monoxide:

C(graph) + 1/2 02(g)  →  CO(g) ΔH3 (5.5)

is difficult ot carry out quantitatively. The carbon monoxide formed will be mixed with some carbon dioxide. Using the fact that enthalpy is a state function we have:

ΔH₁ = ΔH₂ + ΔH₃

and thus we obtain ΔH₃ = - 394 - (- 283) = - 111 kJ

The enthalpy change of a reaction is dependent on temperature, and thus some important information was lacking in the thermochemical equations above. In order to be able to reproduce an experimental enthalpy value, one must know under what temperature conditions the reaction was carried out. Normally enthalpy values are given under the assumption that temperature is the same before and after the reaction. Enthalpies are functions of pressure and temperature, see eq. (2.11). Therefore temperature and pressure must be specified when an enthalpy change is given.

ENTHALPY OF FORMATION :.STANDARD STATE

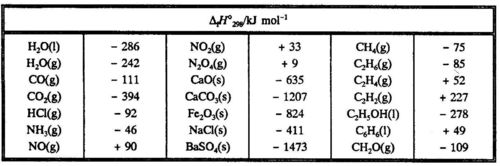
In principle it is not possible to find an absolute value of H (nor of U) for a system. Only enthalpy changes can be found experimentally. It is very inconvenient to list M values for all kinds of different reactions in tables. Instead one finds the enthalpy of formation for various compounds listed in tables. By convention the enthalpy of formation refers to the formatlon of one mole of the compound from the elements in their most stable state at a given temperature and pressure. The enthalpy of formation is given the symbol Δ_fH. The tabulated values referring to a temperature of 25°C or 298 K and a pressure of 1 bar are given the symbol Δ_fH°₂₉₈ and are called standard enthalpies of formation

Thus Δ_fH°₂₉₈ for H₂0 (I) is understood to be the enthalpy change at 25°C when one mole of liquid water is formed from the elements at 1 bar, while Δ_fH°₂₉₈ for H₂0 (g) is the enthalpy change at 25°C when one mole of water vapour at 1 bar is formed from the elements at 1 bar. Water vapour at 1 bar and 25°C will condense spontaneously to liquid water, and thus H₂0(g) (1 bar, 298 K) is unstable.

In Table 5.1 some standard enthalpies of formation are given.

From known enthalpies of formation one can calculate enthalpies of reaction:

In the above example the values of ΔfH°298  for the compounds are found in table 4.1. 

Note that it follows from the convention that the standard enthalpy of formation is equal to zero for an element in its most stable state at 1 bar and 298K.The standard enthalpy of combustion for CH₄(g) is calculated from standard heats of formation, when the chemical equation is- known:

The enthalpy of reaction is the sum of the enthalpies of formation, each multiplied by the stoichiometric eoemclent according to the chemical equation:

(5.6)

where "I are stoichiometric coefficients in the chemical equation. In the above equation V_CH4 =-2, V_CO2 = +1 and V_H2O = +2

TEMPERATURE DEPENDENCE OF ENTHALPY OF REACTI0N

At constant pressure the enthalpy of an element or a compound changes with temperature according to the equation:

dH= C_pdT(5.7)

compare eq. (3.21). The enthalpy of reaction is:

Since the enthalpies of both products and reactants change with temperature according to eq. (4.7), we will also find changes in ΔH with temperature. Tabulated values are usually given at 298 K. You may find the ΔH at the temperature T by integrating eq. (4.7) for each one of the products and each one of the reactants:

(5.9)

Here Δ_r C_P° is the sum of the heat capacities, each multiplied by the stoichiometric coefficient according to the chemical equation:

(5.10)

The V_i are stoichiometric coefficients in the chemical equation, e.g. in eq. V_H2 =-1, V_O2 = -1/2 and V_H2O = +1

The C_P is additive in the same way as ΔH. Generally Δ_rC_P is a function of T. If, however the temperature interval 298 - T is reasonably small (up to a few hundred degrees), Δ_rC_P may be considered constant, and the integral becomes

(5.11)

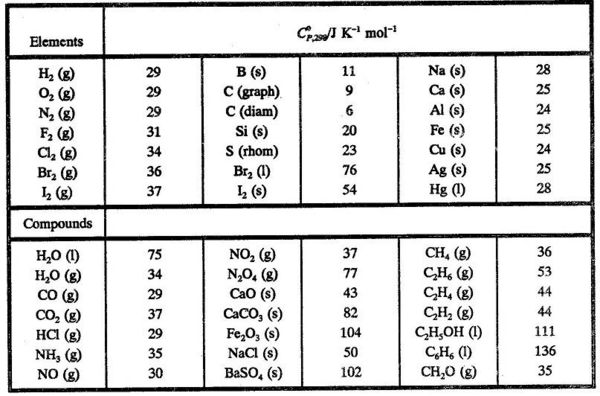
In Table 5.2 are given some standard molar heat capacities.

Using values from Table 5.2 we can find Δ_r C°_P,298 for the reaction

CO (g) + 1/2 O₂(g) → CO₂ (g)

Δ_r C°_P,298 = - 29 - 1/2 x 29 + 37 = -6.5 JK_-1

Using Δ_r H°₂₉₈ = - 283 kJ and eq. (4.9) we can calculateΔ_r H°₂₉₈ for the above reaction:

Δ_r H°₂₉₈=-283 - 0.0065 (598 -298) = -285kJ

Quite often Δ_r C°_P has a very small numerical value as in the above example, and one may considerΔ_r H° as independent of temperature, particularly over small temperature ranges. The temperature dependence of the heat capacity of a substance is often given by an empirical equation of the form:

(5.12)

or, another empirical equation:

C_p = a + bT + cT^-2 ...(5.13)

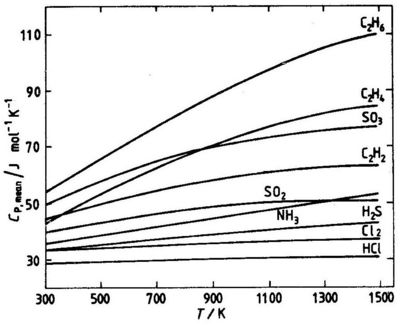
Often the change in enthalpy for a substance is more conveniently calculated from the mean beat capacity, C_p,mean which can be defined as:

(5.14)

where T_o is a reference temperature, usually 298 K. Values of C_p,mean for different temperatures T can be read from graphs, see Fig. 5.2.

The enthalpy change between the temperature T₁ and T₂ can be calculated from the mean heat capacities at the two temperatures:

(5.15)

Fig. 5.2 Mean molar heat capacities for some gases. Reference temperature 298 K

STANDARD ENTHALPIES OF FORMATION OF IONS IN DILUTE AQUEOUS SOLUTIQNS

For liquid (and solid) mixtures the enthalpy of formation depends on concentration. This will be treated in a later chapter in connection with partial molar quantities. We shall discuss already here, however, one type of solutions, namely the dilute electrolyte solutions in water. An aqueous solution is always electrically neutral, the number of positive charges is equal to the number of negative charges. An aqueous solution of an electrolyte will thus contain both positive and negative ions. It is not possible to study the one kind of ions separately. In tables, however, standard enthalpies of formation for single ions are found. In order to show the meaning of these enthalpies, we shall look at an example: When HCl is dissolved in water it is ionized to form H⁺(aq) and CI^-(aq) ions. The enthalpy of formation of HCl (aq) in an infinitely dilute aqueous solution means the enthalpy of formation of H⁺ (aq) and cl^- (aq) simultaneously:

1/2 H₂(g) + 1/2 CI₂(g) + aq = HCl (aq) = H⁺(aq) + CI^-(aq) Δ_fH^o= - 167 kJ^-1

It is not possible to find the contribution from the formation of each type of ion separately. As a convention one has chosen arbitrarily Δ_fH°(H⁺,aq) in infinite dilution equal to zero. This corresponds to a value of - 167 kJ mol^-1 for Δ_fH°(Cl^-,aq).

Assuming the enthalpy of formation for an ion in infinitely dilute solution to be the same independent of other ions present, we can find a conventional standard enthalpy of formation for any ion. Sodium chloride is completely dissociated into ions in an infinitely dilute aqueous solution, and thus Δ_fH°(NaCl,aq)= Δ_fH°(Na⁺,aq) + Δ_fH°(Cl^-,aq).

Hence Δ_fH°(Na⁺,aq) ≠ Δ_fH°(NaCl,aq) - Δ_fH°(Cl^-,aq) = - 407 + 167 = - 240 kJ mol^-1. In a similar way we can find a conventional standard enthalpy of formation for the other ions.

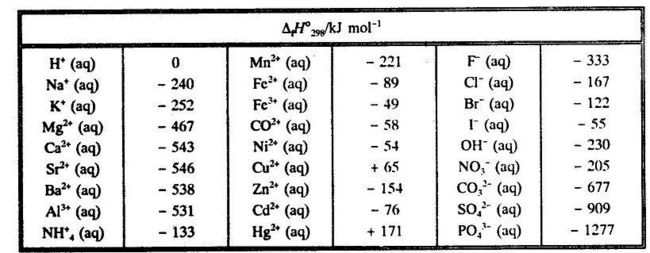
From the conventional standard enthalpies of formation for th~ ions one can find the enthalpy of formation for any strong electrolyte in infinitely dilute aqueous solution. Table 5.3 gives values for some common ions. Table 5.3. Conventional standard enthalpy of formation for ions in infinitely dilute aqueous solution.

FUNDAMENTAL EQUATIONS

Temperature dependence of enthalpy of reaction:

∆_rH^o_T = ∆_rH^o₂₉₈ + ∆_rC_P^odT