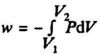The1stLawofThermodynamicsLesson4

THE JOULE - THOMSON EXPERIMENT

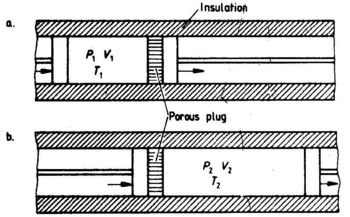
The Joule experiment (see Fig. 1.5) shows that ΔT = 0 when an ideal gas expands under the condition w = O. By careful measurements Joule and Thomson found a small temperature change, usually negative, when a real gas expanded adiabatically through a porous plug. The experimental arrangement is shown in Fig. 4.1.

fig 4.1 Adiabatic expansion of a real gas through a porous plug.

Fig. 4.1. The Joule - Thomson experiment .Adiabatic expansion of a real gas through a porous plug. (a) Initial state. (b) Final state. The pressures P_I and P₂ are kept constant during the expansion. The work supplied to the gas on the left hand side of the porous plug is P₁V_I,and the work carried out by the gas on the right hand side of the porous plug is P₂V₂. The net work received by the gas is:

w = P₁V₁-P₂V₂ (4.2)

The process is adiabatic, q = O. From the first law we have:

 ΔU =U2-U1= w = P1V1-P2V2

which gives:

U₂+P₂V₂=U₁+P₁V₁

From the definition of enthalpy (eq. (4.11)) we obtain:

H₂ = H₁ (4.3)

This means that the enthalpy is constant during the expansion. Joule and Thomson observed that the pressure change, ΔP = P₂ - P_I, gave a change in temperature, ΔT = T₂ - T₁. For most gases at room temperature one observes a positive ratio ΔT/ΔP. The differential:

(4.4)

is called the Joule - Thomson coefficient. The total differential, dH, can be expressed by the Joule ¬Thomson coeffisient. For the function H = f(P, 1), the total differential is expressed by eq. (2.12):

The last term is equal to C_pdT (compare eq. (3.2)). For the Joule - Thomson experiment dH = 0, see eq. (4.3). Dividing eq. (2.12) with dT for dH = 0 we obtain:

or:

(4.5)

Thus the change in enthalpy with changes in P and T is equal to:

dH = - CpμdP + C_pdT (4.6)

This equation is used in calculations of the enthalpy of real gases at high pressures when experimental values are known for the Joule - Thomson coefficient. Joule - Thomson expansion is important in refrigeration and in the liquefaction machine for condensing gases to liquids at very low temperatures.

FUNDAMENTAL EQUATIONS

The first law of thermodynamics:

dU=dq+dw(4.7) (4.7)

For a cyclic process:

(4.8)

The reversible pressure - volume work:

(4.9)

Isothermal reversible pressure - volume work supplied to an ideal gas:

w= -nRT ln (V2/V1)                                                       (4.10) 

Definition of enthalpy:

H= u+pv (4.11)

Heat capacities:

C_v= (∂U/∂T)_y (4.12)

C_p = (∂H/∂T)_p (4.13)