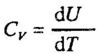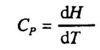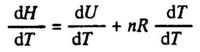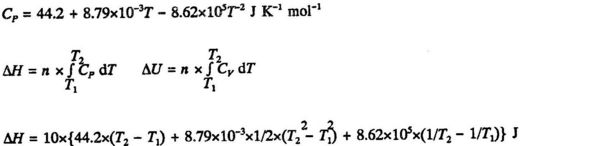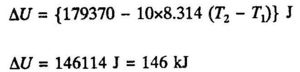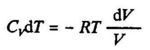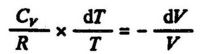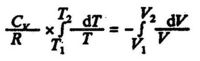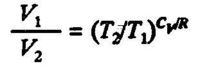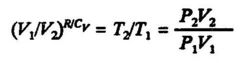The1stLawofThermodynamicsLesson3

HEAT CAPACITIES

When we impart heat to a system and thereby raise its temperature, the average heat capacity in the range ΔT is equal to q/ΔT, and the limit of this ratio, as q is made infinitely small, is called the actual heat capacity at the given temperature. The value of the heat capacity, however, depends on the circumstances under which the system is heated. In order to have a defined heat capacity, we must specify the conditions. The heat capacity, C_v, is defined as the heat capacity at constant volume when there is no work, while C_p is the heat capacity at constant pressure when there is no other work than pressure - volume work. At constant volume (no work) we have q_v =ΔU, and C_v is defined:

(3.1)

The heat capacity at constant pressure (only pressure - volume work) is defined in a similar way. In this case we have q_p= ΔH, and C_p is defined:

(3.2)

These definitions are general and apply to any system, ideal or non-ideal. For ideal gases eqs (3.1, 3.2) can be given a simpler form. As we have seen, the internal energy of an ideal gas is a function of temperature only. Thus the restriction about constant volume is not needed for C_v, compare eq. (2.9), and we have:

(3.3)

Similarly the enthalpy of an ideal gas is a function of temperature only, and the restriction about constant pressure is not needed for C_p, compare eq. (2.6). Thus we have:

(3.4)

For an ideal gas we have:

H = U + PV = U + nRT

Differentiating with respect to T we obtain:

or

(3.5)

In tables we usually find heat capacities per mole. For one mole ideal gas we have C_p = C_v + R.

Example

The change in H and U for 10 mol CO2 (g) when temperature is increased from 100°C to 500°C at constant pressure. In this temperature range the molar heat capacity at constant pressure is known with a high accuracy as a function of temperature. The empirical equation is:

Introducing the values T₁ = (100 + 273.15) K and T₂ = (500 + 273.15) K we obtain:

ΔH = 179370 J = 179 kJ

Neglecting the temperature variation of C_p we obtain ΔH = 176800 J. Unless a very high accuracy is needed, one may neglect the temperature variation of C_p

Assuming that CO₂ behaves like an ideal gas we may introduce:

and we obtain:

REVERSIBLE ADIABATIC EXPANSION OF AN IDEAL GAS 

A process that occurs in an isolated system so that no heat is exchanged with the surroundings is an adiabatic process. Adiabatic processes play an important role in the derivation of equations to be used in the development of the second law of thermodynamics in a mathematical form (Chapter 5). Adiabatic processes have practical importance in connection with air conditioning and refrigeration systems. We may visualize a reversible adiabatic expansion or an ideal gas as shown in Fig. 1.6. The gas is enclosed in an insulated cylinder furnished with an insulated piston that moves without friction. In a similar way as for the isothermal expansion the process is made reversible by adjusting the internal pressure to be very close to the internal pressure all the time (compare Fig. 1.4).

Fig. 3.6 Adiabatic expansion of an ideal gas.

For the adiabatic process q = O. Applying the first law we have:

ΔU=w or dU=dw (3.6)

For one mole of an ideal gas we have by eq. (3.3):

dU= C_vdT (3.7)

where Cv is the molar heat capacity. When the expansion is reversible, we have:

                                                                      (3.8)

Compare eq. (3.6). Equations (3.6, 3.7, 3.8) give:

or, rearranging:

Expanding the gas from a state 1 to a state 2 for constant C_v we have:

which gives by integration:

(3.9)

Taking the antilogarithm we obtain:

hence:

and:

[[image:Formula18.JPG|300px](3.10)                                                            

since C_p = C_v + R for one mole of the ideal gas. Equation (3.10) is frequently written in tbe form:

                                                              (3.9)

The ratio of heat capacities C_p/C_v is often given the symbol y.

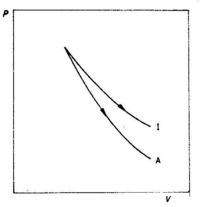
For an adiabatic expansion process PV^y is constant, while for an isothermal expansion process PV is constant. This means that the pressure decreases more for an adiabatic expansion than for an isothermal expansion with the same volume increase, see Fig. 3.7.

Fig. 3.7 Isothermal (I) and adiabatic (A) expansion of an ideal gas.

The work supplied by the reversible adiabatic expansion of an ideal gas for constant C_v is:

                                                                (3.12)