AfroPhysics/Project Planning/Uganda/Good Ideas3 (section)/Astro13/Third Law
MyTitle|Keplers Laws}}
Contents
Newton's gravitation law and circulation
For a body moving in a circular path,The force on it is given by:-
Fz = mω2r
whereby m is the mass of the body, ω the angular speed and r the radius of the circular path.
Here under applies [math]\omega = \frac{2 \pi}{T}[/math]
T is the orbital period of the body.
With the circulation of a planet around the sun the gravitation strength is central Kraft. It is in reverse proportional after Isaac Newton to the square of the distance from the central body:
Fgrav ~ [math] \frac{1}{r^2}[/math]
In addition
Fgrav
proportionally to the two mutually dressing masses M and m:
Fgrav ~ M · m
Together with the Gravitational constant G the Newton's gravitation law results
Fgrav = [math]G \frac{M m}{r^2}[/math]
During a revolution of a light body in the gravity field of a massive body is valid thus
Fz = Fgrav
Fz = Fgrav
[math]m \omega^2 r[/math] = [math]G \frac{M m}{r^2}[/math] and from it [math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G M} [/math]
We recognize a connection between the orbital period and the circle radius - the further far away e.g. the planet from the sun is, the more largely the orbital period. We continue to recognize the fact that the relationship [math]\frac{T^2}{r^3}[/math] depends only on the mass M of the central body, when for all planets, which circle around the sun, which possesses same [math]\frac{4 \pi^2}{G M}[/math] value This had already recognized Kepler in its 3rd Kepler law.
It follows
[math]\frac{T_1^2}{r_1^3} = \frac{T_2^2}{r_2^3}[/math]
[math]\frac{T_1^2}{T_2^2} = \frac{r_1^3}{r_2^3}[/math] Without proof it is communicated that this relationship is valid also for the more general case that the courses of the circulating bodies are ellipses. Then is valid with a1 and a2 as large shaft sections [math]\frac{T_1^2}{T_2^2} = \frac{a_1^3}{a_2^3}[/math]
3. Kepler law
The squares of the orbital periods of the planets behave like the Kuben of their large shaft sections.
A6. Saturn
The ring planet Saturn goes through an ellipse with the large shaft section A = 9.56 AE and the eccentricity = 0,056.
- a) Compute the aphelion and Perihelradius!
- b) How long does Saturn need for a circulation around the sun?
A7. Mars
First expresses planet, Mars, the sun orbits once in 687 days.
- a) Compute its large shaft section (in AE)!
- b) Compute the distance of the earth during the opposition!
A8. Pluto
 Some years ago Pluto its status was denied as planet, since he could clean its orbit not sufficiently of interplanetary subject. It is too small in addition. We add it today to the dwarf planets.
Some years ago Pluto its status was denied as planet, since he could clean its orbit not sufficiently of interplanetary subject. It is too small in addition. We add it today to the dwarf planets.
In the aphelion of its course it is 7423 km far away from the sun. Its speed amounts to 3.67 there km/s. a circulation around the sun happens in 248 years.
- a) Compute the large shaft section (in AE) and the course eccentricity!
- b) How far is Pluto distant in the Perihel from the sun? Which speed does it have there?
A9. Satellites
A television satellite is to stand firmly over a certain point of the earth's surface (“geostationarily”).
- a) Why is this possible only over the Erdäquator? Make in addition a sketch true to scale! Numerical values see c).
- b) How largely does the orbital period have to be T? Compute the angular speed ω!
- c) Compute the flight altitude over the earth's surface! Hint: Proceed thereby from the beginning that the central strength of the circulation is the gravitation strength. (Result: 35873 km = 3.6,104 km)
- d) How long is a radio signal from the satellite to the earth on the way?
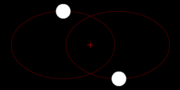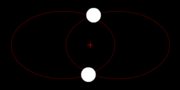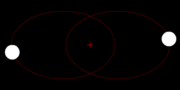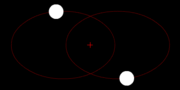
The two body problem
The Newton's gravitation law is symmetrical in the two masses M and m, which describes the physical regularity the fact that both masses dress with the same Kraft mutually i.e. tightens M m just as strongly as m M tightens. Why also should one of the two masses be excellent? This is to be recognized particularly easily to that the two masses could be also alike, thus M = M. who circles then however whom?
This is well-known in astrophysics with double star systems. Correctly, they circle themselves mutually.
How can be?
To understand we need the concept of the center of mass of a system of masses: If one has e.g. two weights M and m, she connects with a firm bar, then one can support the bar at the emphasis and her does not tilt not.
The lever force of the left and right side is alike:
M r1 = m r2
(The bar is regarded as massless.)
If we set the bar in turn, then them can be balanced at the emphasis on the finger.
Two masses in space behave exactly the same, them circle both the emphasis, with the same frequency.
Without proof it is communicated that itself then the equation
[math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G M} [/math] changed too
[math] \frac{T^2}{r^3} = \frac{4 \pi^2}{G (M + m)} [/math] and, generally case, both bodies (to each other similar) ellipses around the emphasis go through.
Two bodies move by mutual attraction around each otherAlso the relative movement of M around m and/or of m around M is again an ellipse with the shaft section A.
[math] \frac{T^2}{a^3} = \frac{4 \pi^2}{G (M + m)} [/math]
We recognize by this equation that the 3rd kg is an approximation, which is valid only for planet masses very small in the comparison to the sun. (This is sufficiently fulfilled. If you compute in addition, like much per cent of the solar mass for instance the mass-richest planet, Jupiter, possesses.)
A10. La Luna
 The Möndin moves on an approximately circular ellipse around the earth.
Note: Look up all necessary sizes in the collection of formulae (see T6)!
The Möndin moves on an approximately circular ellipse around the earth.
Note: Look up all necessary sizes in the collection of formulae (see T6)!
- a) The system moon possesses an emphasis frame calculation you the distance r of the emphasis of the earth center!
- b) Compute the duration of a circulation around the emphasis in days („siderischer “month)! Result: 27.3 D.
- c) Explain on the basis a clear sketch, why between two new moon positions a longer time interval lies (29.5 *D, „synodischer “month)! Note: With Neumond the moon lies between sun and earth!
- d) Explain, why one month 28 - takes 31 days!
Determination of the astronomical unit AU
It was a large challenge to the astronomy to intend the accurate numerical value for the astronomical unit. First astronomers in the whole world evaluated the rare Venusdurchgänge before the sun trigonometrically, achieved thereby however no very large accuracy.
Today the distance can be measured to the Venus directly by means of a radar signal, and then we can compute the absolute value of the astronomical unit from the 3rd kg:
If D is the shortest distance of the Venus of the earth (reached in the lower conjunction), a1 the large shaft section of the Venusbahn, T1 the orbital period of the Venus around the sun, then is valid after Kepler 3 in the comparison with the earth [math]\frac{a_1^3}{a^3} = \frac{T_1^2}{T^2} [/math]
We set
a1 = A D
therein, then we receive the expression after some shapings
[math]a = \frac{d}{1 - (\frac{T_1}{T})^\frac{2}{3}}[/math]
11. Astronomical unit
- a) Derive the above formula for the computation of the large shaft section of the earth (1 AU) from the 3rd kg!
- b) If the Venus is located in lower conjunction to the earth, the running time of a radar signal amounts to the planet and back altogether 273.3 seconds. Compute from it the minimum distance earth - Venus!
- c) Compute with above formula the numerical value of the astronomical unit in km and in m!
- d) Compare with the officially specified value 1 AU = 149,597,870 km!
- e) Note the numerical value 1 AU = 150 million km as good approximation.