Statistical power

Statistical inference as a decision

A statistical hypothesis test assesses the evidence provided by data to refute a null hypothesis, H₀, in favor of an alternative hypothesis, H_a. The goal of the test is to make a decision, based on the evidence from the sample, which agrees with the unknown, true state of the population.

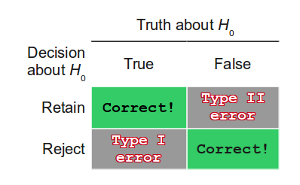
If the alternative hypothesis, H_a, is in fact true in the population—see "Truth about H₀" = "False" in the decision table at right—we will want to design a study so the hypothesis test will have enough power to reject the null hypothesis, H₀, in favor of the alternative—see the bottom right cell in the table.

Motivational example

Suppose you work for a foundation whose mission is to support researchers in mathematics education and your role is to evaluate grant proposals and decide which ones to fund. You receive a proposal to evaluate a new method of teaching high-school algebra. The research plan is to compare the achievement of students taught by the new method with those taught by the traditional method. The proposal contains good theoretical arguments why the new method should be superior and the proposed methodology is sound. In addition to these positive elements, there is one important question still to be answered: Does the experiment have a high probability of providing strong evidence that the new method is better than the standard method even if, in fact, the new method is actually better? It is possible, for example, that the proposed sample size is so small that even a fairly large population difference would be difficult to detect. That is, if the sample size is small, then even a fairly large difference in sample means might not be significant. If the difference is not significant, then no strong conclusions can be drawn about the population means. It is not justified to conclude that the null hypothesis that the population means are equal is true just because the difference is not significant. Of course, it is not justified to conclude that this null hypothesis is false. Therefore, when an effect is not significant, the result is inconclusive. You may prefer that your foundation's money be used to fund a project that has a higher probability of being able to make a strong conclusion.

Understanding power

Power is defined as the probability of correctly rejecting a false null hypothesis—see the bottom right cell in the decision table displayed above. In terms of our example, it is the probability that given there is a difference between the population means of the new method and the standard method, the sample means will be significantly different. The probability of failing to reject a false null hypothesis is often referred to as β—see the top right cell in the decision table, Type II error. Therefore power can be defined as: power = 1 - β.

It is very important to consider power while designing an experiment. You should avoid spending a lot of time and/or money on an experiment that has little chance of finding a significant effect.

High power is desirable. Although there are no formal standards for power, many researchers assess the power of their tests using 0.80 as a standard for adequacy.

Factors affecting power

Statistical power may depend on a number of factors, some of which the researcher may be able to control. The following example will be used to illustrate the various factors.

Suppose a math achievement test were known to be normally distributed with a mean of 75 and standard deviation of σ. A researcher is interested in whether a new method of teaching results in a higher mean. The researcher plans to sample N subjects and do a one-tailed test of whether the sample mean is significantly higher than 75. The researcher specifies the null and alternative hypotheses:

H₀: μ = 75

H_a: μ > 75

Assume that although the experimenter does not know it, the population mean μ is in fact larger than 75. Will the study have enough power to correctly reject the false null hypothesis that the population mean is 75? Let's consider what factors affect power.

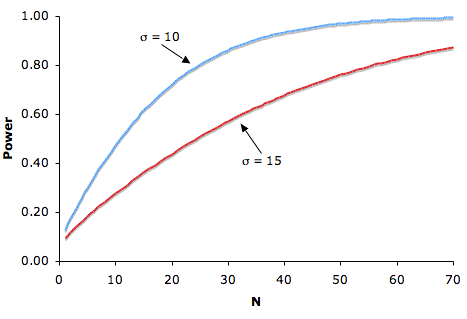
Sample Size

Figure 1 shows that the larger the sample size, the higher the power. With more data, we have more information about [math]\bar {x}[/math], and a better chance of detecting that the population μ is in fact different from the value specified in the null hypothesis. Because sample size is typically under a researcher's control, increasing sample size is one way to increase power. However, it is sometimes difficult and/or expensive to use a large sample size.

Figure 1. The relationship between sample size and power for H₀: μ = 75, when actual μ = 80, for one-tailed tests with α = 0.05, for σ's of 10 and 15.

Standard Deviation

Figure 1 also shows that power is higher when the standard deviation is small as compared to when it is large. For all values of N, power is higher for the standard deviation of 10 than for the standard deviation of 15 (except, of course, when N = 0). Improving the measurement process and sampling from a homogeneous population are two common ways to decrease the standard deviation.

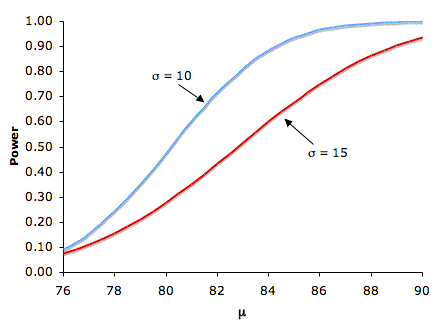
Difference between Hypothesized and True Means

Naturally, the larger the difference between the actual population mean, μ, and the hypothesized value, μ₀, the more likely it is that a study will result in a significant effect, that is, the null hypothesis will be rejected. Figure 2 shows the effect of increasing the difference between the mean specified by the null hypothesis (75) and the population mean, μ, for standard deviations of 10 and 15.

Figure 2. The relationship between power and μ for H₀: μ = 75, for one-tailed tests with α = 0.05, for σ's of 10 and 15.

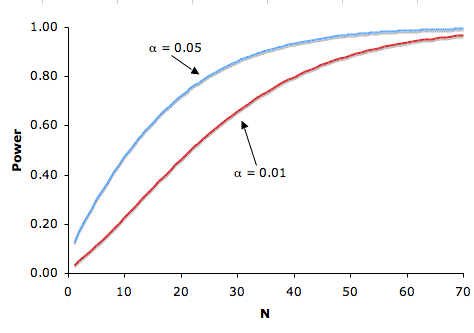
Significance Level

There is a tradeoff between the significance level and power: the more stringent (lower) the significance level, α, the lower the power. Figure 3 shows that power is lower for the α = 0.01 level than it is for the α = 0.05 level. Logically, the stronger the evidence needed to reject the null hypothesis, the lower the chance that the null hypothesis will be rejected in favor of the alternative. When we lessen the chance that the null hypothesis will be rejected, we lessen the power of the statistical test as well.

Figure 3. The relationship between power and significance level with one-tailed tests: : μ₀ = 75, actual μ = 80, and σ = 10.

One- versus Two-Tailed Tests

Power is higher with a one-tailed test than with a two-tailed test as long as the hypothesized direction is correct. For example, a one-tailed test at the 0.05 level has the same power as a two-tailed test at the 0.10 level. A one-tailed test, in effect, raises the significance level, by focusing the collection of evidence in favor of rejecting the null hypothesis in only one direction, rather than two.

Understanding power through simulations

One way to improve your understanding of how the various factors which affect power interact, is to see how differing the values for sample size, standard deviation, mean difference, significance level and one- versus two-tailed tests result in different amounts of power. Remember, a study which can detect important results 80% of the time (power ≥ .80) using a %5 test of significance is a common standard.

The following simulation displays power for a one-sample Z-test of the null hypothesis that the population mean is 50. The red distribution is the sampling distribution of the mean assuming the null hypothesis is true, H₀: μ = 50. The blue distribution is the sampling distribution of the mean based on the "true" population mean. Note the changes in the value of power as you change the values of the various factors.

Simulation 1: Power simulation for one-sample z test, H₀: μ = 50

A second simulation offers an opportunity to interact with the various factors to view, graphically, their combined impact on the power of a two-sample t test. (Don't worry if you have not yet learned about two-sample t tests, focus on the interplay of the factors. The t test will come later.)

Simulation 2: Simulation of of power versus sample size for two-sample t test

When a researcher fails to find evidence for the effects which they believe to be true, we must consider whether the study suffers from lack of power. Better to have explored the study's potential for power during the planning and design process. But to evaluate a study's prospective power, we must specify values for the factors listed above which affect power. Sometimes this is easier said than done.

Computing power

Each type of statistical test employs a different method for calculating power. As it is more important that researchers understand the factors which affect power, and take the time to evaluate prospective power during the design phase of a study, than becoming mired in how to do the specific power calculations, we recommend the use of an online power calculator.

The following is a well-respected site, which includes applets for calculating power for a range of statistical tests. The applets are designed to highlight the interplay among the factors which affect power. Note the commentary on designing studies (e.g., do pilot studies) and the use of power calculations in the lower half of the page.

Power calculator from Russ Lenth, University of Iowa

Once you have determined which statistical test you plan to use in your study, and you have specified your null and alternative hypotheses, you can use the appropriate power calculator to investigate the impact of the factors affecting power, honing in on values for factors such as sample size which will ensure high enough power.

Self-check assessment

Statistical power self-check assessment

Acknowledgements

Portions of this page were adapted from

• Introduction to Power and Factors affecting power at Online Statistics Education: An Interactive Multimedia Course of Study. Project Leader: David M. Lane, Rice University. Retrieved 5 August 2011.
• Statistical power. In Wikipedia, retrieved 7 August 2011.