Simple linear regression/Self-check assessment

Use the following quiz questions to check your understanding of simple linear regression. Note that as soon as you have indicated your response, the question is scored and feedback is provided. As feedback is provided for each option, you may find it useful to try all of the responses (both correct and incorrect) to read the feedback, as a way to better understand the concept.

Interpreting a best fit line

Interpreting a best fit line

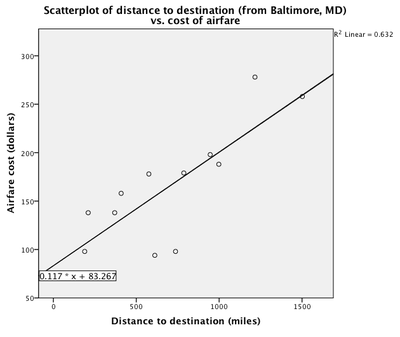
The cost of an airplane flight is related to the distance of the flight. The longer the flight, the more expensive the airfare. Let's take a look at the relationship for a set of data collected on air flights from Baltimore MD to destinations in the US. The scatterplot at right includes the least squares line (the line that best explains the airfare cost based on the distance to destination), and its equation:

• What is the slope of the regression line?
  • .117*x
    • That's not quite right. Recall that the equation of the line has the following form: y = (slope * x) + intercept. In the equation shown in the scatterplot image, the "y=" is not included. Try again.
  • .117
    • That's correct. The slope is the coefficient (number) which is multiplied by each of the x-axis values.
  • -.117
    • That's not quite right. Recall that the equation of the line has the following form: y = intercept + (slope * x). The direction of the relationship is positive, so the slope would be a positive value. Try again.
  • 83.267
    • That's not quite right. Recall that the equation of the line has the following form: y = (slope * x) + intercept. The intercept value in this equation is 83.267. Try again.
• Which of the following is the correct interpretation of the slope of the regression line?
  • For each mile traveled the cost of the airfare decreases by .117 dollars.
    • That's not quite right. Recall that the slope is the change we would expect in the response variable for an increase of 1 unit in the explanatory variable. Note that the direction of the relationship is positive. Try again.
  • A destination which is 1 mile longer is expected to cost 83.267 + .117 dollars more.
    • That's not quite right. Recall that the slope is the change we would expect in the response variable for each 1 unit increase in the explanatory variable; the equation of the line has the following form: y = intercept + (slope * x). Try again.
  • For each mile traveled the cost of the airfare is likely to increase by .117 dollars.
    • That's correct. The slope is the change we would expect in the response variable for an increase of 1 unit in the explanatory variable. A positive slope of .117 for the regression line means that every change of 1 unit in the explanatory variable leads us to expect a change of .117 units in the response variable.
  • For each dollar increase in airfare, the distance traveled increases by .117 miles.
    • That's not quite right. Recall that the slope is the change we would expect in the response variable for an increase of 1 unit in the explanatory variable. In this example, which variable is the explanatory variable and which is the response? Try again.
• The distance from Baltimore to Tampa is 852 miles. Is it reasonable to use the linear regression equation to predict the cost of the airfare? If so, what is the predicted cost?
  • Yes.
    • That's correct. The distance is within the range of distances used to establish the linear regression equation. It is reasonable to make the assumption that the established regression equation could be used for predicting the airfare cost for this distance. Using the regression line to predict the cost, we would calculate [math]\hat{y} = .117(852)+83.267 = 182.951[/math], suggesting the predicted cost would be $183.
  • No.
    • That's not quite right.
• The distance from Baltimore to San Francisco is 2450 miles. Is it reasonable to use the linear regression equation to predict the cost of the airfare? If so, what is the predicted cost?
  • Yes.
    • That's not quite right.
  • No.
    • That's correct. The distance is well outside the range of distances used to establish the relationship. The calculated regression line is a summary of the linear relationship in the range of included distances only. There is no justification for the assumption that the relationship continues to be linear for larger distances.

• What is the most common criterion used to determine the best-fitting line to describe the relationship between two quantitative variables?
  • The line that minimizes the sum of squared distances from the data points to the line, in the y (vertical) direction.
    • That's correct. The most common criterion used to determine the best-fitting line is the line that makes the sum of squares of the vertical distances of the data points from the line as small as possible. This line does not need to go through any of the actual data points, and it can have a different number of points above it and below it.
  • The line that minimizes the sum of squared distances from the data points to the line, in the x (horizontal) direction.
    • That's not quite right. We use the regression line to predict a y-value (response) given an x-value (explanatory), so we want to minimize the error in predicting y, that is, the distance from the data point to the line in the y direction. Try again.
  • The line that goes through the most points
    • That's not quite right. The most common criterion for determining the best fit line does not need to go through any of the actual data points, rather it attempts to minimize the error in predicting the response variable, given values of the explanatory variable.
  • The line that has the same number of points above it as below it
    • That's not quite right. The most common criterion for determining the best fit line does not need to have the same numbers of points above and below the line, rather it attempts to minimize the error in predicting the response variable, given values of the explanatory variable.
• The mean of X is 3 and the mean of Y is 7. The regression line that predicts Y from X must pass through the point (3,7).
  • True.
    • That's correct. Someone who scored the mean on variable X would be predicted to score the mean on variable Y.
  • False.
    • That's not quite right. Someone who scored the mean on variable X would be predicted to score the mean on variable Y.

Understanding linear regression

• Suppose it is possible to predict a person's score on Test B from the person's score on Test A. The regression equation is: [math]\hat{B} = 1.5 A + 9.5[/math]. The predicted score for the person on Test B given the person got a 40 on Test A would be 70 (round the score to an integer).
  • That's correct. Plug [math]A=40[/math] into the equation to find [math]\hat{B} = 1.5(40) +9.5 = 69.5[/math], which rounded is 70.
  • That's not quite right. Plug [math]A = 40[/math] into the equation [math]\hat{B} = 1.5 A + 9.5[/math] and solve for [math]\hat{B}[/math]. Be sure to round your result to a whole integer. Try again.