Simple harmonic motion
Contents
- 1 OBJECTIVES
- 2 DEFINITION
- 3 EXAMPLES OF SIMPLE HARMONIC MOTION
- 3.1 Mass spring systems
- 3.1.1 Mass attached to spring on a horizontal smooth surface
- 3.1.2 Mass between two springs on a horizontal smooth surface
- 3.1.3 Mass attached to a vertical spring
- 3.1.4 Mass attached to two vertical springs connected in parallel
- 3.1.5 Mass attached to two vertical springs connected in series
- 3.1.6 Simple pendulum
- 3.1.7 Liquid oscillating in a U-tube
- 3.1 Mass spring systems
- 4 Applications of s.h.m
- 5 Revision questions
OBJECTIVES
|
By the end of this topic the reader should be able to;
|
DEFINITION
| Simple harmonic motion is that kind of periodic motion in which the acceleration of the body along the path of motion is directed towards a fixed point in the line of motion and directly proportional to the displacement of the body from a fixed point. |
Definitions of common terms
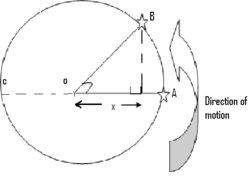
Suppose the mass is initially at A and that after a time t it is at B. During this time the radius r of the circle sweeps through an angle θ. The motion of the mass from A round the circle is equivalent to the motion of a mass from A to C and then back to A. The distance X is the displacement of the mass from the centre of motion at any time t. The distance OB ( r ) is theamplitude of motion.
The acceleration in s.h.m is expressed as =-ω2x,……………………………………………………..(i) where ω is the angular velocity.
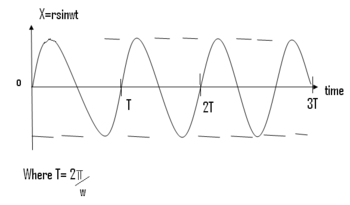
Solving the differential equation (i) yields two solutions; X = rsin( ωt +Є )…………………………….................................(ii)
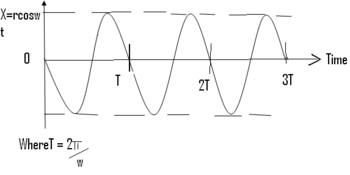
and X =rcos( ωt+Є )……………………………………………………………………………………………………………..(iii)
which clearly are functions of t. where Є is a constant called the phase constant whose values are determined by the initial conditions. If we consider X= rcos(ωt+Є) and assume that
- If X = r at t=0, then cosЄ = 1 this implies that Є=0, in this case (iii) simplifies to X=rcos ωt.
- If X =0 at t = 0, then cosЄ = 0this implies that Є =90degrees or .
(iii) then becomes X = rcos( ωt + 90 )=- rsinωt. Thus the motions of X=rcosωt and X = rsinωt differ in phase by 90degrees. A sketch of X= rcosωt against time t is of the form:
A sketch of X= rsinωt against time t is of the form:EXAMPLES OF SIMPLE HARMONIC MOTION
Mass spring systems
Mass attached to spring on a horizontal smooth surface
Mass between two springs on a horizontal smooth surface
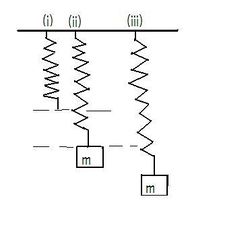
Mass attached to a vertical spring
In (ii) the system is in equilibrium. The tension T in the spring is equal to the weight mg of the body. i.e T = mg ..................................................................................................(1) where g is the acceleration due to gravity. From Hooke's law, T = ke where k is the spring constant and e is the extension produced in the spring by the mass m. Therefore from (1) ke = mg....................................................................(2) Suppose the mass is displaced downwards by an amount x and then released.The new tension T' is now given by T' = k(e + x). Restoring force on the mass is given by T' - mg = -ma.............................(3) where a is the acceleration of the system upwards. Negative sign shows the the restoring force and the displacement x increase in opposite directions. Combining (1), (2) and (3) yields K(e + x) - ke = -ma or -ma = kx..................................................................(4) therefore acceleration a of the system is given by a = -(k/m)x. ............................. ...............(5) Equation (5) clearly shows that an oscillating spring mass system in the vertical exhibits simple harmonic motion since its equation of motion is of the form of the fundamental equation of simple harmonic motion.