Secondary Mechanics/Page8: Newton's Laws
machine translation
Inertial forces in different reference systems
Thought experiment: cars piggyback
A (small) car is on a (large) experimental cars. An observer A stands next to the attempt in a dormant reference system. Observer B sits on the large experimental cars. Now the big car from the peace process.
We can imagine, for example, we stand as an observer in an accelerating B subway, while A on the platform remains back, and the small car is a skateboard in the central aisle of the subway.
What happened?
Correct: The little car is not accelerating. He remains in a calm observer to the big wagon driven away under him, then he falls down. He does not finally accelerating force.
Observer B, on the other hand registered an acceleration of the small car to the rear, and it closes on a force F accelerating. If he wants, he can force them with a knife measure. It is the so-called inertial force of Wägelchens, because it has caused by the inertia of the small car.
In the dormant A system of the force F is not.
We note:
Inertial forces enter only in the accelerated reference systems.
Task 3.1
A passenger in a carousel experiences depending on what system of reference is his movement, different forces.
- A) reference system of a dormant observer outside the carousel
- B) reference system in the passenger carousel
Draw on each passenger forces and arrange them the names of force (centrifugal), and Central force (centripetal). What power is a force of inertia?
Now, we want the accelerating forces, or the inertial forces quantify.
Preliminaries:
Obviously, there is a link between the mass of accelerated body, and its acceleration is acting force. For example, we need more power, a serious body to speed up as a slight.
Example: It is much easier for a bicycle jo like a car.
In plain English: The bigger the mass m of a body, the more force F is required to accelerate a certain distance.
Caution: This is only a Je-Desto statement, a monotonous relationship between the sizes A and B: If A (mass), including B (the force), when C (acceleration) is remains constant.
It is also:
M bigger ⇒ F = bigger in a constant
But also:
F bigger ⇒ m higher at constant a =
So together
For a = constant is: m bigger ⇔ larger F
Task 3.2: Formulate appropriate monotony relations
For the case
- A) m = constant
- B) F = constant
2 Newton Act (NG2)
Now we want the relationship between the force, mass and acceleration quantitatively investigated. All three sizes can be directly or indirectly measure, which gives us the opportunity, systematic testing for them. We question the nature!
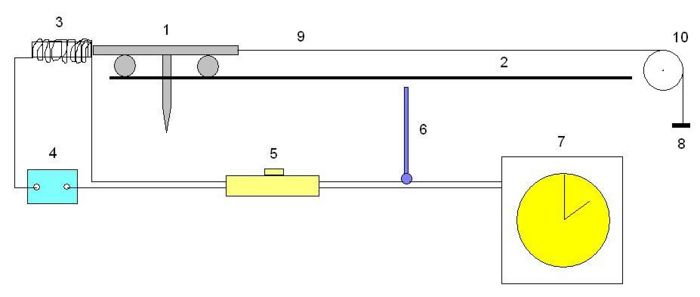
Consider first the experimental setup:
The core of the arrangement is a roller coaster with a driving test car known mass m. He is supported by the strength of a weight accelerates, produced by a cord, which runs through a pulley, to draw him. The acceleration of the car is made of driving time, the car needed to establish a distance of 1.00 meters to go. This time we measured with an electric clock, which triggered at the start and after 1.00 m automatically stopped.
- Experimental car
- Role roadway
- Electromagnet
- Power Source
- Touchswitch
- Snap switch
- Electric stopwatch
- Weight
- Cord
- Pulley
Details of the experimental design: the road is slightly tilted to compensate for the friction. The car will start with an electromagnet in the starting position held. With a switch is now also the circuit for the electromagnets and off the circuit for electrical pm. The car drives off, the clock is running. Through the vehicle ferrying the snap button at the end of the trail, the timing is automatically stopped. The weight can be for different tractive forces in increments of 10 grams.
Test series 1
M = constant, is the missing link between the force F and the acceleration a.
Student contribution: experimental results
(| Class = "wikitable" | -- ! Bulk of the weight in grams ! T in the (Group 1) ! T in the (group 2) ! A m / s 2 </ sup> (group 1) ! A m / s 2 </ sup> (group 2) | -- | 10 | 3.49 | 3.4 | 0,164 | 0,173 | -- | 20 | 2.70 | 2.33 | 0,274 | 0,368 | -- | 30 | 1.96 | 2.15 | 0,520 | 0,432 | -- | 40 | 1.69 | 1.86 | 0,700 | 0,578 | -- | 50 | 1.54 | 1.53 | 0,843 | 0,854 |)
Task 3.3: experimental analysis
Enter the measured values of the two groups in an appropriate diagram, draw a straight line balancing the measurement values as well as possible meet and confirm that the relationship
The acceleration grows in proportion to a pulling force F.
Test series 2
Prerequisite: F = constant
Now we Zuggewichts the mass of the same and change the mass of the car, we are certain mass attach additional documents. We measure the return journey times for a distance of 1.00 m from the rest and calculate the resulting accelerations.
Result:
The acceleration is inversely proportional to the mass.
That means, for example: double mass, half acceleration.
Test series
Prerequisite: a = constant
We determine the outcome of the trial and thought confirm it in the experiment. Double we, for example, the mass, as is the double attraction needed to have the same acceleration. (In any thoughts half of the double mass separated accelerated.)
Result:
The need to speed traction force is proportional to the mass.
So
1st F ~ = m with a constant
2nd 1 / m at a ~ F = constant
3rd F ~ m with a = constant
Let the three relations in a so true
F ~ m * a
The formula is so important that according to her the SI unit system has been adjusted. It is the proportionality factor 1 (!) Consequently,
2nd Newton Act (NG2)
F = m * a
In words: Force is mass times acceleration
It is the unit's equation
1 N = 1 kg * m / s 2 </ sup>
Calculation example :< br />
A train consisting of a locomotive and 8 equal wagons, speeding from the booth with a = 0.50 m / s 2 </ sup>.
This requires the locomotive of the mass 84 tons a tensile force of 122 kN up. Which has a mass wagon?
Solution:
[math] F = m * a \lt/ math\gt \ltbr /\gt
\ltmath\gt M = \ frac (F) (a) \lt/ math\gt \ltbr /\gt
M = 244 t \ltbr /\gt
'''M \ltsub\gt wagon \lt/ sub\gt = 20 t'''
[[Mechanics11/Seite9 | to next page]][/math]